Rumus Panjang Garis Singgung Persekutuan Dua Lingkaran

Pada pembahasan kali ini, kita akan membahas panjang garis singgung persekutuan dalam maupun garis singgung persekutuan luar dua lingkaran.
 

1. Rumus Panjang Garis Singgung Persekutuan Dalam Dua Lingkaran

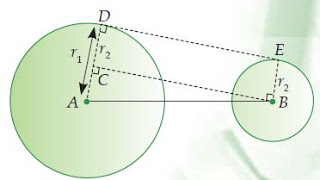
Perhatikan gambar di bawah ini! Lingkaran A berpusat di A dengan jari-jari AC = r1. Lingkaran B berpusat di B dengan jari-jari BE = r2.
 

AB adalah jarak kedua titik pusat lingkaran (s). CE adalah garis singgung persekutuan dalam dua lingkaran, dimana CE⊥AC. Melalui titik B, kita dapat menarik garis BD yang sejajar dengan garis CE. (BD//CE), sehingga CD = BE = r2, dan ∠ADB = 90^o.

Maka ΔADB adalah segitiga siku-siku, sehingga berlaku teorema Phythagoras, yaitu:
AB² = AD² + BD2
BD² = AB² – AD²
        = AB² – (AC + CD)²
        = s² – (r1 + r2)2

Karena BD//CE dan ∠ADB = ∠ACE = 90^o, maka CE = BD. Jadi, CE² = s² – (r1 + r2)². Sehingga, dapat kita simpulkan bahwa panjang garis singgung persekutuan dalam dua lingkaran adalah:

 d² = s² – (r1 + r2)2

dengan r1 > r2, dan
d : panjang garis singgung persekutuan dalam dua lingkaran
s : jarak antara kedua pusat dua lingkaran
r1 : jari-jari lingkaran pertama
r2 : jari-jari lingkaran kedua
 

2. Rumus Panjang Garis Singgung Persekutuan Luar Dua Lingkaran

Perhatikan gambar di bawah ini! Lingkaran A berpusat di A dengan jari-jari AD = r1. Lingkaran B berpusat di B dengan jari-jari BE = r2.
 

AB adalah jarak kedua titik pusat lingkaran (s). DE adalah garis singgung persekutuan luar dua lingkaran, dimana DE⊥AD. Melalui titik B, dapat ditarik garis BC yang sejajar garis DE (BC//DE), sehingga BE = CD = r2, dan ∠ACB = 90^o.

Maka ΔACB adalah segitiga siku-siku, sehingga berlaku teorema Phythagoras,
AB² = AC² + BC2
BC² = AB² – AC²
        = AB² – (AD – CD)²
        = s² – (r1 – r2)2

Karena BC//DE dan ∠ACB = ∠ADE = 90^o, maka DE = BC. Jadi, DE² = s² – (r1 – r2)². Maka panjang garis singgung persekutuan luar dua lingkaran dirumuskan:

 l² = s² – (r1 – r2)2

dengan r1 > r2, dan
l : panjang garis singgung persekutuan luar dua lingkaran
s : jarak antara kedua pusat dua lingkaran
r1: jari-jari lingkaran pertama
r2: jari-jari lingkaran kedua
 

Contoh Soal

Panjang garis singgung persekutuan dalam dua lingkaran adalah 15 cm. Panjang jari-jari lingkaran yang besar adalah 6 cm. Jika jarak antara kedua titik pusat sama dengan 17 cm, hitunglah panjang jari-jari yang lingkaran kecil!

Penyelesaian:
d = 15 cm,
r1 = 6 cm,
s = 17 cm

d² = s² – (r1 + r2)2
15² = 17² – (6 + r2)2
225 = 289 – (6 + r2)2
(6 + r2)² = 289 – 225
               = 64
6 + r² = √64
6 + r² = 8
r² = 8 – 6 = 2 cm

Jadi panjang jari-jari lingkaran kecil adalah 2 cm.