Persamaan Umum Lingkaran (Kedudukan Titik Terhadap Lingkaran)
.jpg)
Titik dan lingkaran yang terletak dalam satu bidang datar mempunyai kududukan yang dibedakan dalam tiga kondisi. Kondisi tersebut adalah titik di dalam lingkaran, titik pada lingkaran, dan titik di luar lingkaran. Tiga kondisi inilah yang akan dibahas pada materi tentang kedudukan titik terhadap lingkaran. Untuk menentukan letak titik terhadap lingkaran dapat secara mudah terlihat jika digambarkan dalam bidang kartesius. Seperti halnya gambar lingkaran yang berpusat di titik O(0,0) dengan jari-jari 3 cm dan titik dengan koordinat (1, 2) berikut.
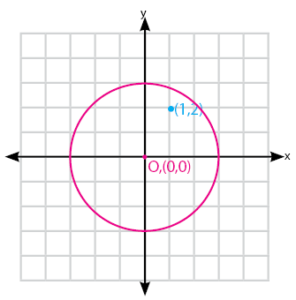
Dengan sangat mudah, sobat dapat menentukan bahwa titik berada di dalam lingkaran. Namun, hal ini tidak efektif karena diperlukan waktu yang cukup banyak. Bagaimana untuk kedudukan titik (1, 3) pada lingkaran dengan pusat (1, 2) dan jari-jari 2 cm? Apakah letak titik (1, 3) berada di dalam lingkaran, pada lingkaran, atau di luar lingkaran? Menggambarkan lagi lingkaran dan titik bukan merupakan jalan keluar yang terbaik, ada solusi lainnya. Solusi lain untuk mengetahui kedudukan titik terhadap lingkaran dapat diperoleh dengan menggunakan kriteria yang melibatkan rumus persamaan lingkaran dan titik yang bersangkutan. Barikut ini adalah penjelasan lebih jauh tentang kriteria untuk mengetahui kedudukan titik terhadap lingkaran.
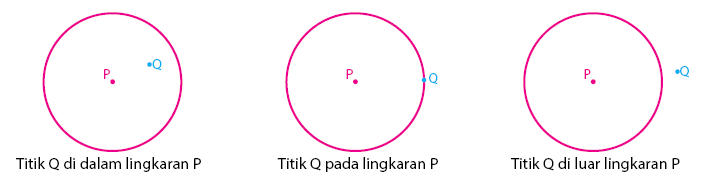
Kriteria Kedudukan Titik Terhadap Lingkaran dengan Persamaan Umum 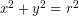
Bentuk persamaan lingkaran 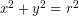 memiliki pusat di titik O(0, 0) dengan panjang jari-jarinya adalah
memiliki pusat di titik O(0, 0) dengan panjang jari-jarinya adalah  . Letak suatu titik terhadap lingkaran yang memiliki bentuk umum
. Letak suatu titik terhadap lingkaran yang memiliki bentuk umum 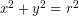 dapat dilihat pada daftar berikut.
dapat dilihat pada daftar berikut.
- Titik terletak di dalam lingkaran jika
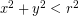
- Titik terletak pada lingkaran jika
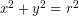
- Titik terletak di luar lingkaran jika
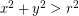
Kriteria Kedudukan Titik Terhadap Lingkaran dengan Persamaan Umum 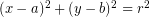
Persamaan lingkaran dengan bentuk 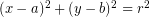 memiliki pusat di titik P(a, b) dengan panjang jari-jarinya adalah
memiliki pusat di titik P(a, b) dengan panjang jari-jarinya adalah  . Letak suatu titik terhadap lingkaran yang memiliki bentuk umum
. Letak suatu titik terhadap lingkaran yang memiliki bentuk umum 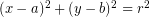 dapat dilihat pada daftar berikut.
dapat dilihat pada daftar berikut.
- Titik terletak di dalam lingkaran jika
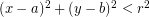
- Titik terletak pada lingkaran jika
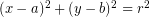
- Titik terletak di luar lingkaran jika
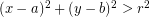
Kriteria Kedudukan Titik Terhadap Lingkaran dengan Persamaan Umum 
Persamaan lingkaran dengan bentuk 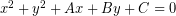 memiliki pusat di titik
memiliki pusat di titik 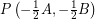 dengan panjang jari-jarinya adalah
dengan panjang jari-jarinya adalah 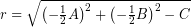 .
.
Kedudukan titik terhadap lingkaran yang memiliki bentuk umum 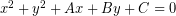 dapat dilihat pada daftar berikut.
dapat dilihat pada daftar berikut.
- Titik terletak di dalam lingkaran jika
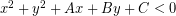
- Titik terletak pada lingkaran jika
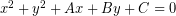
- Titik terletak di luar lingkaran jika
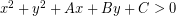
Contoh Soal dan Pembahasan
Contoh 1: Contoh Soal dan Pembahasan Kedudukan titik di Dalam Lingkaran
Selidiki kedudukan titk (3, 1) pada lingkaran  !
!
Pembahasan:
Substitusi titik (3, 1), nilai x = 3 dan y =1, pada persamaan  .
.
![Rendered by QuickLaTeX.com \[ (3)^{2} + (1)^{2} - 4(3) + 2(1) - 4 = 9 + 1 - 12 + 2 - 4 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-21935bed736ddf5ceb849afb99cd4b74_l3.png)
![Rendered by QuickLaTeX.com \[ = 9 + 1 - 12 + 2 - 4 = -4 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-09706ab9288c39f75dd6e4781bcddbbf_l3.png)
Karena 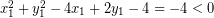 , maka letak titik (3, 1) berada di dalam lingkaran
, maka letak titik (3, 1) berada di dalam lingkaran  .
.
Contoh 2: Contoh Soal dan Pembahasan Kedudukan titik pada Lingkaran
Selidikilah letak titik (3, 4) pada lingkaran dengan persamaan  !
!
Pembahasan:
Substitusi titik (3, 4), nilai x = 3 dan y = 4, pada lingkaran  .
.
![Rendered by QuickLaTeX.com \[ (3)^{2} + (4)^{2} = 9 + 16 =25 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-99d4c9e029e0e2732916e662fa51f8d4_l3.png)
Karena nilai  , maka titik (3, 4) terletak pada lingkaran
, maka titik (3, 4) terletak pada lingkaran  .
.
Contoh 3: Contoh Soal dan Pembahasan Kedudukan titik di Luar Lingkaran
Seldikilah letak titik (5, 3) pada lingkaran yang memiliki persamaan 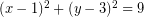 !
!
Pembahasan:
Substitusikan titik (5, 3), nilai x = 5 dan y = 3, ke persamaan 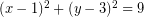 !
!
![Rendered by QuickLaTeX.com \[ (5 - 1)^{2} + (3 - 3)^{2} = 4^{2} + 0^{2} = 16 + 0 = 16 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-6ee5055316fb56cfc37d7efe60bc0d56_l3.png)
Karena 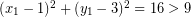 , maka letak titik (5, 3) adalah di luar lingkaran
, maka letak titik (5, 3) adalah di luar lingkaran 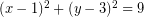 .
.
Sekian pembahasan mengenai kedudukan titik terhadap lingkaran. Terimakasih, semoga bermanfaat.