Fungsi Komposisi dan Fungsi Invers Lengkap dengan Contoh Soal dan Pembahasan

Otakers, untuk kalian ketahui proses pembuatan buku terjadi dalam 2 tahap. Tahap pertama yaitu dimulai dari tahap editorial dan tahap kedua yaitu tahap produksi. Di dalam tahap editorial, naskah akan kemudian di edit serta di layout menjadi file yang siap untuk dicetak. Berikutnya, file diolah dalam tahap produksi mencetaknya supaya menjadi sebuah buku. Nahh, tahukah kalian bahwa sebenarnya proses ini merupakan salah satu bentuk penerapan dari Fungsi komposisi matematika lho !

Fungsi Komposisi

Fungsi komposisi adalah penggabungan dari suatu operasi dua jenis fungsi f(x) dan juga g(x) sehingga mampu menghasilkan suatu fungsi baru.

Adapun rumus untuk fungsi komposisi, yaitu:

Rumus Fungsi Komposisi

Operasi untuk fungsi komposisi tersebut biasa dinotasikan dengan penggunakan huruf atau simbol “o” atau sering dibaca sebagai komposisi ataupun bundaran. Fungsi baru inilah yang bisa terbentuk dari menggabungkan f(x) dan g(x) yaitu:

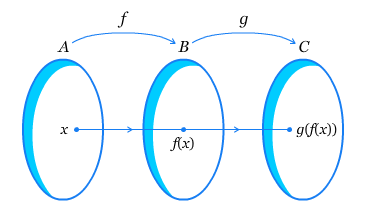
1. (f o g) (x) yang berarti g dimasukkan ke f

2. (g o f) (x) yang berarti f dimasukkan ke g

Fungsi tunggal merupakan suatu fungsi yang dapat dinotasikan dengan penggunakan huruf “f o g” atau dapat dibaca “f bundaran g”.

Lalu Fungsi (f o g) (x) = f (g (x)) → fungsi g (x) dikomposisikan sebagai fungsi f (x)

Sementara itu, “g o f” dibaca sebagai fungsi g bundaran f. Sehingga, “g o f” merupakan fungsi f yang diselesaikan terlebih dahulu dari fungsi g.

Baca Juga :

Apa Perbedaan Fungsi Injektif, Surjektif dan Bijektif ?

Pengertian Relasi, Fungsi, Domain,Kodomain dan Range

Dari rumus di atas, dapat kita ketahui bahwa:

Apabila f: A → B ditentukan dengan menggunakan rumus y = f(x)

Apabila g: C → D ditentukan dengan menggunakan rumus y = g(x)

Sehingga, akan kita peroleh hasil fungsi g dan f yaitu:

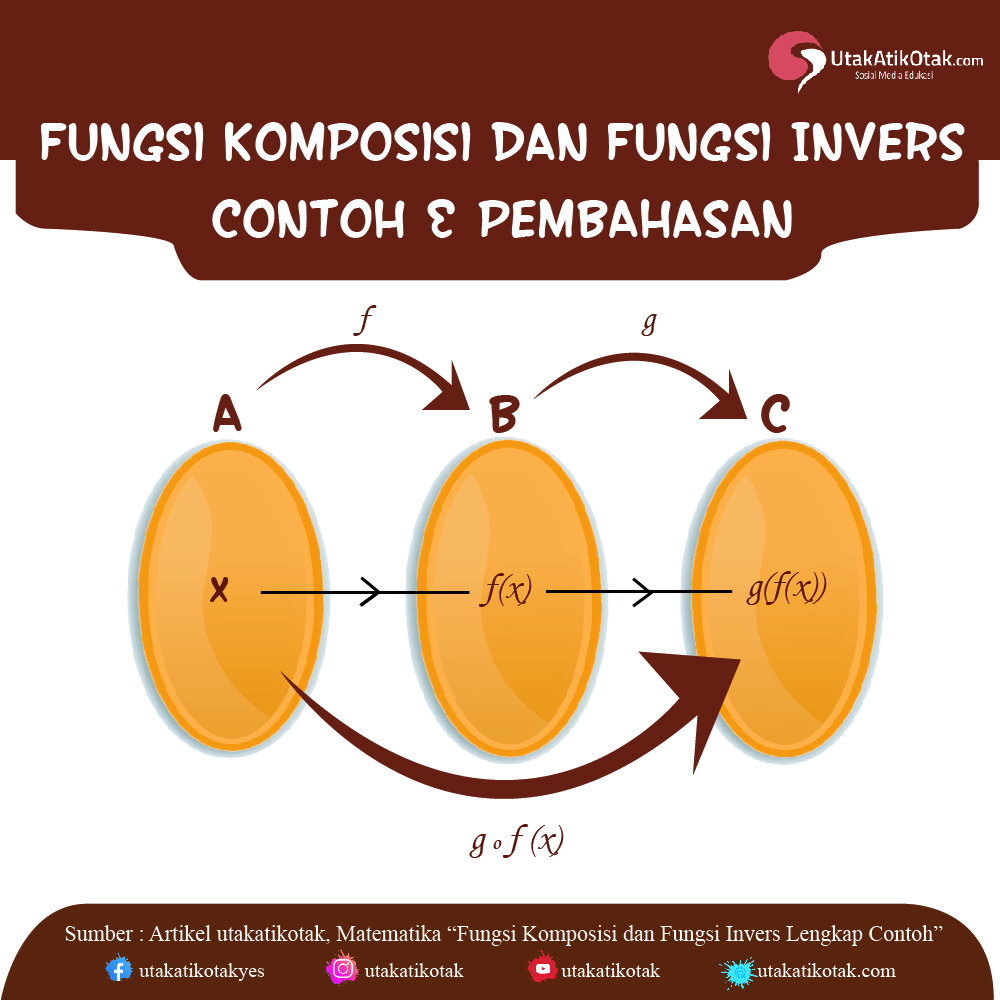
h (x) = (g o f) (x) = g (f(x))

Dari definisi di atas maka bisa kita simpulkan jika fungsi yang melibatkan fungsi f dan g bisa kita tulis seperti berikut ini:

• (g o f) (x) = g(f(x))
• (f o g) (x) = f(g(x))

Untuk memahami uraian di atas, berikut ini adalah contoh soal untuk fungsi komposisi yang sederhana

Contoh soal fungsi komposisi

Sifat Sifat Fungsi Komposisi

Berikut beberapa sifat dari fungsi komposisi, diantaranya adalah sebagai berikut:

Apabila f: A → B, g: B → C, h: C → D, maka akan berlaku:

Sifat Fungsi Komposisi

1. Tidak berlaku sifat komutatif, (f ◦ g) (x) ≠ (g ◦ f) (x).
2. Berlaku sifat asosiatif, (f ◦ (g ◦ h)) (x) = ((f ◦ g) ◦ h) (x).
3. Adanya unsur identitas (l)(x), (f ◦ l) (x) = (l ◦ f) (x) = f (x).

Aljabar Fungsi

1. Penjumlahan f dan g

(f + g) (x) = f (x) + g (x)

2. Pengurangan f dan g

(f – g) (x) = f (x) – g (x)

3. Perkalian f dan g

(f.g) (x) = f (x). g (x)

4. Pembagian f dan g

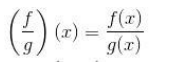
Fungsi Invers

Fungsi invers terjadi sebab adanya sebuah fungsi yang dinotasikan dengan f (x) serta memiliki relasi pada setiap himpunan A ke setiap himpunan B.

Sehingga akan menjadi sebuah fungsi invers yang dinotasikan dengan f-1 (x) yang tak lain mempunyai relasi dari himpunan B ke setiap himpunan A.

Sehingga, fungsi invers diperoleh dari f : A → B yang berubah menjadi f^-1: B → A sehingga daerah asal atau domain f (x), menjadi daerah kawan atau kodomain menjadi daerah hasil atau range f^-1 (x) yakni himpunan A. Begitu pula sebaliknya terjadi pada himpunan B.

Fungsi invers atau yang juga dikenal sebagai fungsi kebalikan adalah sebuah fungsi yang berkebalikan dari fungsi asalnya.

Sebuah fungsi f mempunyai fungsi invers (kebalikan) f^-1 jika f adalah fungsi satu-satu dan fungsi pada (bijektif). Hubungan tersebut bisa dinyatakan seperti berikut:

(f^-1)^-1 = f

Simplenya, fungsi bijektif berlangsung pada saat jumlah anggota domain sama dengan jumlah anggota kodomain.

Tidak terdapat dua atau lebih domain berbeda dipetakan ke kodomain yang sama. Serta pada setiap kodomain mempunyai pasangan di domain. 

Sebagai contoh, f fungsi yang memetakan x ke y, sehingga bisa kita tulisakan menjadi y = f(x), maka f-1 merupakan fungsi yang memetakan y ke x, ditulis x = f^-1(y).

Misalnya f: A →B fungsi bijektif. Invers fungsi f merupakan fungsi yang mengawankan pada masing-masing elemen B dengan tepat satu elemen pada A.

Terdapat 3 tahapan untuk menentukan fungsi invers, antara lain:

1. Ubahlah bentuk y = f (x) menjadi bentuk x = f (y).
2. Tuliskan x sebagai f^-1(y) sehingga f^-1(y) = f (y).
3. Ubahlah variabel y dengan x sehingga akan didapatkan rumus fungsi invers f^-1(x).

Rumus Fungsi Invers

1. f^-1 (x) adalah invers dari fungsi f(x)

2. Menentukan fungsi invers: mengganti f (x)= y = …” menjadi “f ^-1 (y)= x = …”

3. Hubungan sifat fungsi invers dengan fungsi komposisi:

1. (f ◦ f^-1) (x)= (f ^-1 ◦ f) (x)= l (x)
2. (f ◦ g)^-1 (x)= (g^-1 ◦ f^-1) (x)
3. (f ◦ g) (x)= h (x)→ f (x)= (h ◦ g ^-1) (x)

Nahh otakers, itulah pembahasan lengkap Fungsi Komposisi dan Fungsi Invers Lengkap dengan Contoh Soal dan Pembahasan. Semoga dapat bermanfaat yah !