Contoh Soal Median Data Tunggal dan Kelompok

Apa arti median ?

Median adalah nilai tengah dari data yang telah disusun berurutan mulai dari yang terkecil sampai dengan yang terbesar. Secara matematis median dilambangkan dengan Me yang dapat dicari dengan cara sebagai berikut.

Median Data Tunggal

Rumus Median Data Tunggal (nilai tengah)

Ketika kalian ingin mencari nilai tengah atau Median pada data tunggal pastikan dulu banyaknya data yang akan dicari. Ada dua ketentuan bagaimana cara mencari Median yaitu perhatikan banyak data yang disajikan apa jumlah data ganjil atau genap.

Median jika jumlah data (n) ganjil

Median jika jumlah data (n) genap

Keterangan:

Me = Median

n = jumlah data

x = nilai data

 

Contoh Soal Median Data Tunggal 1:

Pada suatu kelas didapatkan hasil nilai ulangan siswa sebagai berikut

65,70,85,90,80,60,70,80,80,80,50

median data tersebut adalah...

Pembahasan :

Karena banyaknya data adalah ganjil sebanyak 11, maka penghitungan median menggunakan rumus median untuk data ganjil. Cara penghitungannya adalah sebagai berikut.

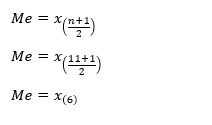
Dari rumus matematis di atas, diperoleh bahwa median adalah x₆. Untuk mengetahui x₆, maka data harus diurutkan terlebih dahulu. Hasil pengurutan data adalah sebagai berikut.

50, 60, 65, 70, 70, 80, 80, 80, 80, 85, 90

Setelah diurutkan maka diperoleh nilai median x₆ = 80

 

Contoh Soal Median Data Tunggal 2 :

Median dari 34,35,35,36,40,37,43,35,35,37 adalah

Pembahasan :

Karena banyaknya data adalah genap sebanyak 10, maka penghitungan median menggunakan rumus median untuk data genap. Cara penghitungannya adalah sebagai berikut.

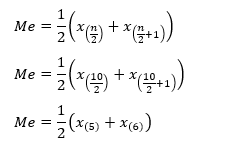
Untuk mengetahui nilai median dari hasil diatas, maka data harus diurutkan terlebih dahulu. Hasil pengurutan data adalah sebagai berikut.

34, 35, 35, 35, 35, 36, 37, 37, 40, 43

Setelah diurutkan maka diperoleh data x₅ = 35 dan x₆ = 36

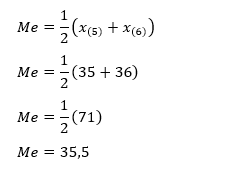
maka diperoleh nilai median 35,5

 

Median Data Kelompok

Pada data tunggal, penghitungan median cukup mudah. Data diurutkan berdasarkan nilai datanya mulai dari yang terkecil sampai yang terbesar. Kemudian median bisa diketahui langsung dari nilai tengah urutan data tersebut.

Namun pada data berkelompok, cara tersebut tidak bisa digunakan. Data berkelompok merupakan data yang berbentuk kelas interval, sehingga kita tidak bisa langsung mengetahui nilai median jika kelas mediannya sudah diketahui.

Rumus Median data Kelompok

Oleh karena itu, kita harus menggunakan rumus berikut ini.

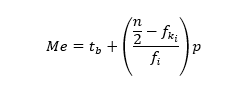
Me = median

t_b = batas bawah median

n = jumlah data

f_ki = frekuensi kumulatif data sebelum kelas median

fi = frekuensi data pada kelas median

p = panjang interval kelas

Contoh Soal Median Data Kelompok 1

Data Nilai ujian Matematika kelas 11 sudah digolongkan kedalam tabel seperti di bawah ini

Interval Nilai	fi
40-49	1
50-59	4
60-69	8
70-79	14
80-81	10
90-99	3
Total	40

 

Pembahasan :

Karena banyaknya data sejumlah 40, maka setengah dari data tersebut adalah 20 dan selanjutnya mencari kelas median.

Interval Nilai	fi	fk
40-49	1	1
50-59	4	5
60-69	8	13
70-79	14	27
80-81	10	37
90-99	3	40
Total	40	40

• Kelas median berada diinterval nilai 70-79 karena frekuensi kumulatif di interval tersebut memuat nilai setengah dari data.
• Tepi bawah t_b = 69,5
• Panjang kelas p = 10
• Banyak data n = 40
• Frekuensi kumulatif sebelum kelas median f_ki = 13
• Frekuensi kelas median f_i = 14

Sehingga, nilai median adalah :

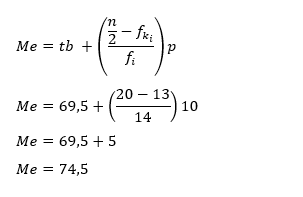
Contoh Soal Median Data Kelompok 1

Berikut ini adalah data berat badan 50 orang mahasiswa jurusan statistika yang telah dikelompokkan ke dalam kelas-kelas interval berat badan. Hitunglah median berat badan mahasiswa tersebut.

Berat Badan (kg)	Jumlah Mahasiswa
60 – 64	4
65 – 69	12
70 – 74	15
75 – 79	10
80 – 84	4
85 – 89	5
Total	50

 

Pembahasan:

Hitung terlebih dahulu frekuensi kumulatif dari data tersebut. Selanjutnya tentukan kelas interval yang memuat median data.

Berat Badan (kg)	Frekuensi (fi)	Frekuensi Kumulatif (fk)
60 – 64	4	4
65 – 69	12	16
70 – 74	15	31
75 – 79	10	41
80 – 84	4	45
85 – 89	5	50
Total	50

 

Karena jumlah data (mahasiswa) adalah 50, maka median data terletak pada data ke-25 dan data ke-26.

Dari hasil penghitungan frekuensi kumulatif di atas, dapat kita ketahui bahwa median terletak pada kelas interval ketiga, yaitu kelas interval 70 – 74. Frekuensi kelas interval dimana median terletak adalah 15, sedangkan frekuensi kumulatif sebelum kelas interval median adalah 16. Selain itu dapat kita ketahui juga bahwa panjang interval adalah 5 dan batas bawah kelas median adalah 69,5.

Secara matematis, nilai-nilai tersebut dapat kita tulis dalam notasi sebagai berikut.

t_b = 69,5

n = 50

fki = 16

fi = 15

p = 5

Dengan menggunakan rumus median data berkelompok di atas, kita dapat mengetahui median berat badan siswa.

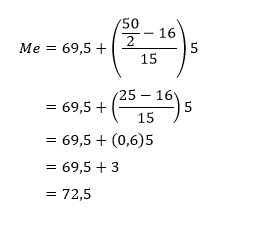
Dengan demikian median berat badan mahasiswa jurusan statistika adalah 72,5 kg.

Nahh agar kalian dapat memahami dengan cara visual, kalian bisa menyimak ulasan dalam video di bawah ini yah