Rumus Volume Kubus dan Luas Permukaan

Hai otakers,

Buat kalian yang masih bingung untuk menghitung rumus-rumus dari bangun ruang yang satu ini, coba deh kalian pahami satu per satu pembahasan di artikel ini. Memahami rumus-rumus dalam kubus sepertinya tidak boleh dilewati karena hampir dalam semua soal berkaitan dengan bangun ruang akan muncul soal tentang kubus.

 

Rumus Volume Kubus dan Luas Permukaan

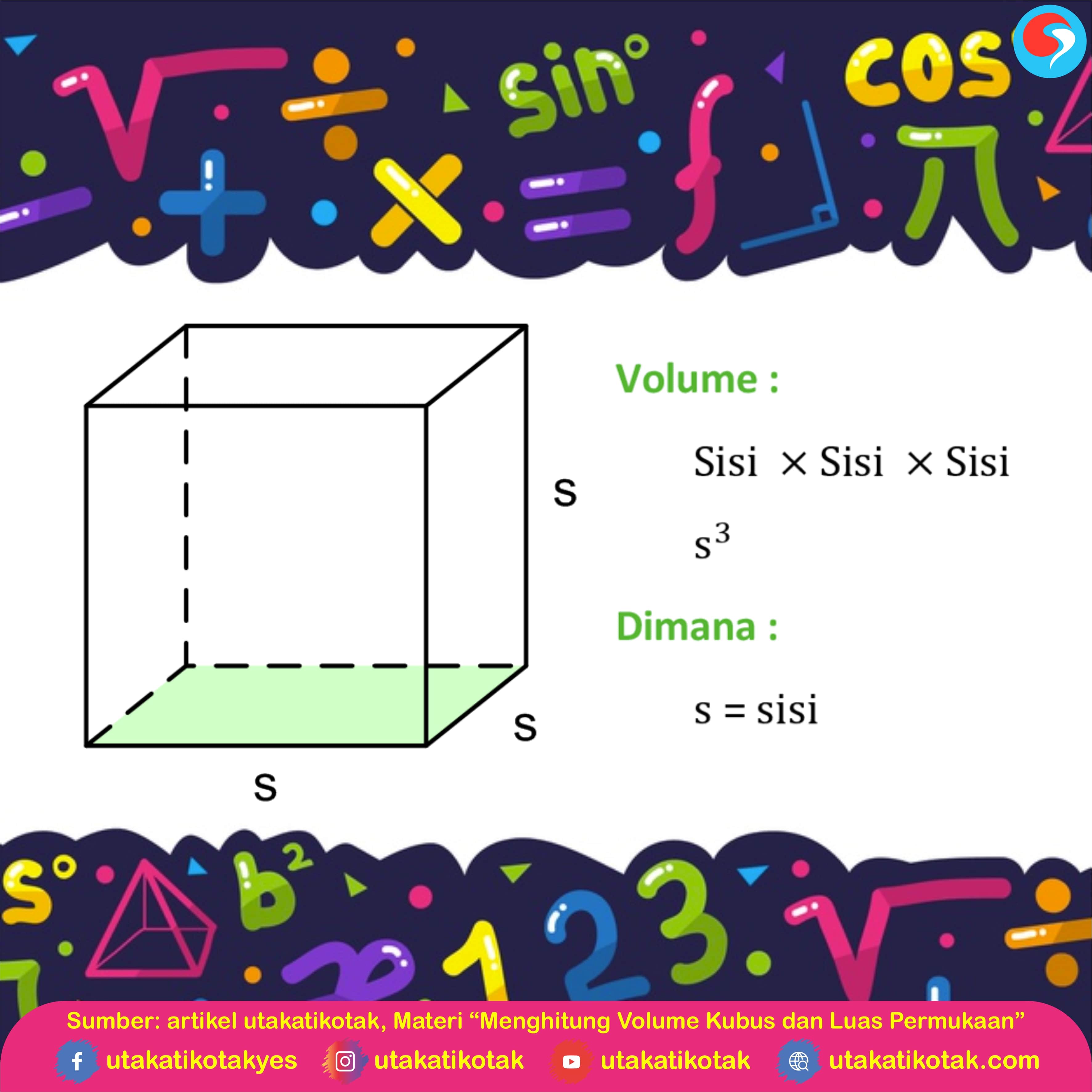
Besarnya volume kubus merupakan perpaduan antara perkalian dari sisi panjang, lebar serta tinggi. Sedangkan Luas permukaan kubus adalah jumlah luas seluruh sisi atau bidang pada bangun ruang tersebut. Ukuran rusuk dari sebuah kubus semuanya sama yaitu dilambangkan dengan huruf “r”. Dengan demikian rumus menghitung volume kubus dan luas permukaan bisa dinyatakan sebagai berikut ini:

Volume = r x r x r atau Volume = r³

Luas permukaan = 6 r²

Bila yang diketahui adalah luas perseginya maka kalian harus menghitung terlebih dahulu panjang sisi kubus tersebut. Diketahui rumus dari luas persegi adalah rusuk x rusuk sehingga untuk mencari panjang sisinya anda bisa dengan menghitung akar pangkar dua dari luas persegi tersebut.

Setelah kalian memperoleh panjang sisi maka selanjutnya masukkan pada rumus volume seperti yang sudah disampaikan di atas.

Tips Menyelesaikan Soal Volume Kubus dan Luas Permukaan

1. Terdapat beberapa nilai pangkat tiga yang harus anda ketahui dan hafal sehingga memudahkan anda menyelesaikan soal volume kubus.
2. Perhatikanlah satuan volume tersebut yaitu pangkat tiga dari satuan panjang rusuknya. Untuk satuan panjang milimeter (mm) maka satuan volumenya yaitu mm³. Untuk satuan panjang rusuk centimeter (cm) maka satuan volmenya yaitu cm³ dan seterusnya.

Contoh soal

1.] Sebuah kubus memiliki panjang sisi sebesar 30 cm, maka hitunglah volume kubus tersebut.

Jawab :

Volume kubus = r x r x r
= 30 x 30 x 30
= 27.000 cm ^3.

Jadi volume kubus tersebut adalah 27.000 cm³

Baca Juga :

Volume Limas dan Contoh Soal

Rumus Volume dan Luas Permukaan Bangun Ruang Lengkap

2.] Pak Reza sedang membuat sebuah bak mandi yang berbentuk kubus dengan panjang rusuk-rusuknyanya 100 cm. Pak Reza ingin mengisi bak mandi tersebut menggunakan air hingga penuh. Maka tentukan berapa literkah air yang dibutuhkan oleh Pak Reza untuk mengisi bak mandi tersebut sampai penuh?

Jawab :

Volume kubus = r x r x r
= 100 x 100 x100
= 1.000.000 cm³ = 1.000 dm³ = 1.000 liter

Jadi untuk memenuhi bak mandi tersebut maka Pak Reza harus menyiapkan air sebanyak 1000 liter.

3.] Sebuah kubus memiliki volume sebesar 125 cm^3. Hitunglah berapa panjang rusuk dari kubus tersebut !
Jawab :
Volume = 125 cm³
125 = r³
r³ = 125
r = 5 cm

Jadi Panjang rusuk dari kubus tersebut adalah 5 cm

 

Menghitung Volume Kubus dan Luas Permukaan Jika Rusuknya Diperpanjang

Lalu, bagaimana mencari volume dan luas permukaan jika sebuah Kubus dengan rusuk yang ada akan diperpanjang atau diperpendek dengan ukuran tertentu.

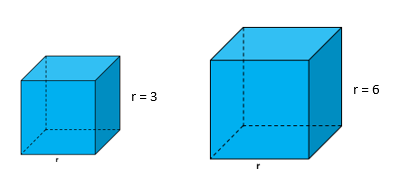
Kubus a.

Luas permukaan = 6 r² = 6×3² = 6×9 = 54 cm²

volume = r³ = 3³ = 27 cm³

Kubus b.

Luas permukaan = 6r² = 6×6² = 6×36 = 216 cm²

volume = r³ = 6³ = 216 cm³

Selanjutnya perhatikanlah panjang rusuk kubus a dan b, dimana panjang rusuk kubus b merupakan 2× panjang rusuk kubus a, sehingga kita akan memperoleh sebagai berikut.

panjang rusuk kubus b = 2 × panjang rusuk kubus a

Kita misalkan,

Panjang rusuk a = x = 3

Panjang rusuk b = y = 2x

Luas permukaan kubus b

Lp (b)  = 6 . r_b² = 6 . y²

Lp (b)  = 6 . (2x)²

Lp (b)  = 6 . (2.3)²

Lp (b)  = 6 . (6)²

Lp (b)  = 6 . 36

Lp (b)  = 216 cm²

Volume Kubus b

Volume b = y³

volume b = (2x)³

volume b = (2 . 3)³

volume b = 2³ . 3³

volume b = 8 . 27

volume b = 216 cm³

Dari uraian tersebut maka kita dapat menyimpulkan sebagai berikut.

Jika panjang rusuk suatu kubus = r, luas permukaan = L serta volumenya = V, selanjutnya panjang rusuk kubus tersebut diperbesar atau diperkecil k kali maka

a. L (baru) = 6 (k . r)²

    L (baru) = 6 k²r²

    L (baru) = k² . (6 r²)

    L (baru) = k² L

   dimana L (baru) = luas permukaan kubus setelah diperbesar atau diperkecil dan L = Luas permukaan semula

b. V (baru) = (k . r)³

    V (baru) = k³ . (r³)

    V (baru) = k³ . V

    dimana V (baru) = volume kubus setelah diperbesar atau diperkecil dan L = volume semula

Dengan menggunakan cara yang sama kita dapat menemukan Luas Permukaan serta Volume Balok jika ukuran panjang, lebar serta tingginya berubah. Sehingga jika suatu balok memiliki panjang = p, lebar = l, tinggi = t, luas permukaan = L, serta volume = V. Selanjutnya balok tersebut ukurannya diubah menjadi panjang = ap, lebar = bl, tinggi ct dengan a,b,c konstanta positif. a, b, c merupakan pengali yang bisa saja besarnya sama tergantung soal. Maka kita peroleh sebagai berikut.

a. L (baru) = 2 [ (ap×bl) + (bl×ct) + (ap×ct) ]

    L (baru) = 2 [ ab (p×l) + bc (l×t) + ac (p×t) ]

b. V (baru) = ap × bl × ct

    V (baru) = abc (p×l×t)

    V (baru) = abcV

    jika a = b = c maka luas serta volumenya menjadi sebagai berikut.

a. L (baru) = 2 [ ab (p×l) + bc (l×t) + ac (p×t) ]

    L (baru) = 2 [ a.a(p×l) + a.a(l×t) + a.c(p×t) ]

    L (baru) = 2 [ a² (p×l) + a² (l×t) + a² (p×t) ]

    L (baru) = 2 [ a² ((p×l) + (l×t) + (p×t)) ]

    L (baru) = a² × [ 2 ((p×l) + (l×t) + (p×t)) ]

    L (baru) = a² Lp

b. V (baru) = abcV

    V (baru) = a³V

    dengan L (baru) = luas permukaan balok setelah diubah ukurannya

                 V (baru) = volume balok setelah diubah ukurannya

                     L        = luas permukaan balok semula

                     V       = volume balok semula

Contoh soal.

1) Sebuah kubus memilki panjang rusuk 9 cm, selanjutnya rusuk tersebut diperkecil menjadi 1/3 kali panjang rusuk semula. Berapakah volume kubus setelah diperkecil ?

Penyelesaian :

Diket :

r = 8 cm

k = 1/3

Dit : V (baru) ?

Jawab :

V = r³ = 9³ = 729 cm³

V (baru) = k³ V

V (baru) = (1/3)³ × 729

V (baru) = (1/27) x 729

V (baru) = 27 cm³

Jadi volume kubus setelah diperkecil rusuknya menjadi setengah kali yaitu 27 cm³

 

2) Pak Hadi ingin memperbesar ukuran kolam ikan miliknya yang berbentuk seperti kubus dengan Panjang rusuk-rusuk 6 meter menjadi 2 kali lipat dari semula. Berpakan luas permukaan kolam tanpa penutup dan hitunglah volume air dan ikan yang muat didalamnya ?

Penyelesaian :

Diket :

r = 6 cm

k = 2

Dit : L (baru) = ?

Jawab :

L (baru) = k² L

               = 2² (5 . r²)

               = 4 (5 . 6²)

               = 4 (5 . 36)

               = 4 (180) = 720 m²

V = r³ = 6³ = 216 m³

V (baru) = k³ V

V (baru) = (2)³ × 216

V (baru) = (8) x 216

V (baru) = 1728 m³

Untuk lebih memahami tentang volume kubus dan luas permukaan kubus, kalian simak ulasan dalam video berikut

 

Nahh, setelah ini semoga kalian bisa memahami pembahasan beserta contoh soal diatas ya otakers.