Soal dan Pembahasan Bangun Ruang Lengkap

Soal – soal bangun ruang

1. Disediakan kawat yang panjangnya 6 m akan dibuat kerangka balok berukuran 13 cm x 9 cm x 8 cm. Berapa banyak kerangka balok yang bisa dibuat dari kawat tersebut ...

Jawab :

Panjang kawat = 6 m = 600 cm

1 Keranka = 4 x ( p + l + t) x 1cm

= 4 x (13 + 9 + 8)x 1cm

= 4 x 30 x 1 cm

= 120 cm

Jadi, kerangka balok yang bisa dibuat sebanyak = 600 cm : 120 cm = 5 balok

 

2. Sebuah balok berukuran panjang = (3x + 2) cm , lebar = (x + 5)cm, dan tinggi = (2x – 4)cm. Jika jumlah rusuknya 156 cm, maka nilai x adalah

Jawab :

Jumlah rusuk = 4 x ( p + l + t) x 1cm

156 cm = 4 x (3x + 2 + x + 5 + 2x – 4) x 1 cm

156 cm = 4 x (6x +3) x 1cm

156 cm / 4 = 6x +3

39 – 3 = 6x

36 = 6x 

 x  = 36 / 6  

    = 6

Baca Juga :

Materi Jaring Jaring Balok

Rumus Volume Balok & Contoh Soal

Rumus Balok – Luas Sisi, Volume, Diagonal Ruang Bidang

3. Jumlah panjang sebuah rusuk adalah 96 cm. Luas permukaan kubus adalah

Jawab :

Kerangka = 12 x rusuk

96 cm = 12 x rusuk

Rusuk = 96 cm / 12

Rusuk = 8 cm

Luas Permukaan Kubus = 6 x sisi

                                       = 6 x (8 x 8) x 1 cm²

                                       = 6x 64 cm²

                                       = 384 cm²

 

4. Suatu balok memiliki luas permukaan 516 cm². Jika panjang dan lebar masing-masing 15 cm dan 6 cm, maka tinggi balok tersebut adalah

Jawab :

Luas permukaan balok = 2 x (( p x l ) + (p x t) + (l x t))

516 cm =  2 x (( p x l ) + (p x t) + (l x t))

516 / 2 = (90 + 15t + 6t)

258      = (90 + 15t + 6t)

258 – 90= 15t + 6t

168       = 21 t

    t        = 168 / 21

    t        = 8 cm

 

5. Alas sebuah prisma berbentuk segitiga siku-siku dengan panjang sisi 3cm, 4 cm, 5cm. Jika luas permukaan prisma adalah 108 cm². Maka tinggi prisma tersebut adalah

Jawab :

Misal, a = 3 cm , t segitiga = 4 cm, c = sisi miring = 5 cm

Luas alas dan penutup = 2 x ( ½ x a x t segitiga)

                                     = 2 x (½ x 3 x 4)

                                     = 2 x 6

                                     = 12 cm²

Luas sisi tegak = (a x T) + (t x T) + (c x T)

                         = ( a + t + c) x T

                         = ( 3 + 4 + 5) x T

                         = (12 T) cm²

Luas permukaan = Luas alas + Luas Sisi Tegak

108 cm² = 12 cm² + 12 T

108 cm² - 12 cm² = 12 T

96 cm² = 12 T

​​​​​​​     T     = 96 cm² /12

     T     = 8 cm

 

6. Alas sebuah limas beraturan berbentuk persegi dengan panjang sisi 5 cm dan tinggi bidang segitiga tegaknya adalah 10cm. Luas permukaan limas tersebut adalah

Jawab :

Luas alas = sisi x sisi = 5 x 5 = 25 cm²

Luas sisi tegak = 4 x Luas segitiga

= 4 x (1/2 x 5 x 10)

= 4 x 25

= 100 cm²

Jadi, Luas permukaan = Luas alas + Luas sisi tegak

= 25 cm² + 100 cm²

= 125 cm²

 

7. Sebuah prisma alasnya berbentuk belah ketupat dengan panjang diagonal 16 cm dan 12 cm. Luas permukaan prisma tersebut jika tingginya 12 cm adalah

Jawab :

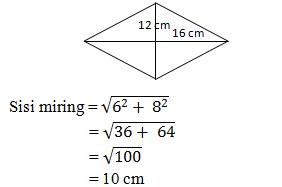
Luas alas = Diagonal 1 x Diagonal 2

= 12 cm x 16 cm

= 192 cm²

Luas sisi tegak = 4 x(sisi miring x t)

= 4 x (10 x 12) x 1cm²

= 4 x 120 cm²

= 480 cm²

Luas permukaan = Luas alas + luas sisi tegak

= 192 cm² + 480 cm²

= 672 cm²

 

8. Volume balok yang berukuran 13cm x 15cm x 17cm adalah 

Jawab :

Volume = p x l x t

= 13 x 15 x 17

= 3315 cm³

 

9. Halimah membuat model balok padat dari bahan gipsum dengan luas alas 200cm² dan tingginya 9cm. Harga ipsum per liter adalah Rp 15.000,00 . Rupiah minimal uang halimah yang harus dikeluarkan untuk membuat model balok tersebut adalah

Jawab :

Volume = luas alas x tinggi

= 200cm² x 9 cm

= 1800 cm³ = 1,8 dm³ = 1,8 liter

 

Minimal uang Halimah = Volume x harga per liter

= 1,8 liter x Rp 15.000,00

= Rp 27.000,00

 

10.  Suatu kolam renang diisi penuh oleh air yang memiliki panjang 9cm dan lebar 6 cm. Kedalaman air pada ujung dangkal adalah 1m dan terus melandai hingga 4 m pada ujung dalam. Berapa literkah volume air dalam kolam ...

Jawab :

Volume 1 balok dengan tinggi = 1 m

V = p x l x t

= 9 x 6 x 1

= 54 m³

Volume 2 berbentuk prisma segitiga dengan tinggi 3 meter

V = luas alas x tinggi

= 9 cm x 6 cm x 3 cm

= 162 cm³

Baca juga : 

Kumpulan Soal dan Pembahasan Bangun Ruang