Contoh Soal Pembagian Suku Banyak dan Metode Horner

Pengertian Derajat Polinomial

Derajat merupakan pangkat tertinggi dari variabel yang terdapat pada suatu suku banyak. Jika suku banyak ditulis a_nxⁿ + a_n-1x^n-1+ … + a₁x + a₀, maka derajat dari suku banyak tersebut adalah n. bagaimanakah derajat suku banyak dari hasil bagi?

Teorema Sisa

Jika suatu suku banyak F(x) dibagi oleh (x – k) maka sisanya adalah F(k)

Jika pembagi berderajat n maka sisanya berderajat n – 1

Jika suku banyak berderajat m dan pembagi berderajat n, maka hasil baginya berderajat m – n 

• Metode Pembagian Suku Banyak

contoh :

Jika P(x) = 3x³ – 4x² + kx + 4 habis dibagi (3x + 2), maka nilai k adalah ...

1. Pembagian Biasa

Jawab :

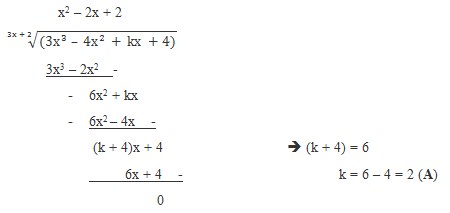
Sehingga hasil baginya: H(X) = x² – 2x + 2, sisanya S(x) = 0

1. Cara Horner/skema

cara ini dapat  digunakan untuk pembagi berderajat 1 atau pembagi yang dapat difaktorkan menjadi pembagi-pembagi berderajat 1

Cara:

• Tulis koefisiennya saja → harus runtut dari koefisien xⁿ, x^{n – 1}, … hingga konstanta (jika ada variabel yang tidak ada, maka koefisiennya ditulis 0)

Contoh: untuk 4x³ – 1, koefisien-koefisiennya adalah 4, 0, 0, dan -1 (untuk x³, x², x, dan konstanta)

• Jika koefisien derajat tertinggi P(x) ≠ 1, maka hasil baginya harus dibagi dengan koefisien derajat tertinggi P(x)
• Jika pembagi dapat difaktorkan, maka:

Jika pembagi dapat difaktorkan menjadi P₁ dan P₂, maka S(x) = P₁.S₂ + S₁

Jika pembagi dapat difaktorkan menjadi P₁, P₂, P₃, maka S(x) = P₁.P₂.S₃ + P₁.S₂ + S₁

Jika pembagi dapat difaktorkan menjadi P₁, P₂, P₃, P₄, maka S(x) = P₁.P₂.P₃.S₄ + P₁.P₂.S₃ + P₁.S₂ + S₁

dan seterusnya

Untuk soal di atas,

P(x) = 3x³ – 4x² + 2x + 4

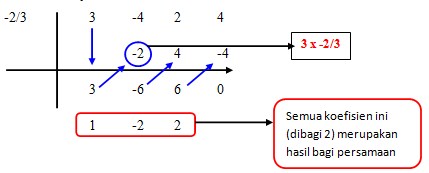
P₁: 3x + 2 = 0 → x = - 2/3

Cara Hornernya:

Jadi untuk  S(x) =  0, H(x) = x² – 2x + 2

Teorema Faktor

Suatu suku banyak F(x) mempunyai faktor (x – k) jika F(k) = 0 (sisanya jika dibagi dengan (x – k) adalah 0)

Catatan: jika (x – k) adalah faktor dari F(x) maka k dikatakan sebagai akar dari F(x)

Tips

1. Untuk mencari akar suatu suku banyak dengan cara Horner, dapat dilakukan dengan mencoba-coba dengan angka dari faktor-faktor konstanta dibagi faktor-faktor koefisien pangkat tertinggi yang akan memberikan sisa = 0.

Contohnya :untuk x³ – 2x² – x + 2 = 0, faktor-faktor konstantanya: ±1, ±2, faktor-faktor koefisien pangkat tertinggi: ±1. Sehingga, angka-angka yang perlu dicoba: ±1 dan ±2untuk 4x³ – 2x² – x + 2 = 0, faktor-faktor konstantanya: ±1, ±2, faktor-faktor koefisien pangkat tertinggi: ±1, ±2, ±4. Sehingga, angka-angka yang perlu dicoba: ±1, ±2, ±1/2, ±1/4.

2. Jika jumlah koefisien suku banyak = 0, maka pasti salah satu akarnya adalah x = 1.

3. Jika jumlah koefisien suku di posisi genap = jumlah koefisien suku di posisi ganjil, maka pasti salah satu akarnya adalah x = –1

Baca Juga :

Metode Pembagian Suku Banyak / Polinomial

Perhatikan contoh berikut :

Tentukan penyelesaian dari x³ – 2x² – x + 2 = 0?

Jawab :

Faktor-faktor dari konstantanya, yaitu 2,  adalah ±1 dan ±2 dan faktor-faktor koefisien pangkat tertingginya, yaitu 1, adalah ±1, sehingga angka-angka yang perlu dicoba: ±1 dan ±2

Karena jumlah seluruh koefisien + konstantanya = 0 (1 – 2 – 1 + 2 = 0), maka, pasti x = 1 adalah salah satu faktornya, atau dengan soal sebelumnya seperti di bawah ini

Jadi untuk P(x) = 3x³ – 4x² + 2x + 4 = ( 3x + 2) (x² - 2x + 2)

 Memiliki satu faktor yaitu = (3x + 2) atau x = - 2/3  

Jadi himpunan penyelesaiannya: {–1/2}

Sifat Akar-Akar Suku Banyak

Pada persamaan berderajat 3:

ax³ + bx² + cx + d = 0 akan mempunyai akar-akar x₁, x₂, x₃

dengan sifat-sifat:

Jumlah 1 akar: x₁ + x₂ + x₃ = – b/a

Jumlah 2 akar: x₁.x₂ + x₁.x₃ + x₂.x₃ = c/a

Hasil kali 3 akar: x₁.x₂.x₃ = – d/a

Jumlah 1 akar: x₁ + x₂ + x₃ + x₄ = – b/a

Jumlah 2 akar: x₁.x₂ + x₁.x₃ + x₁.x₄ + x₂.x₃ + x₂.x₄ + x₃.x₄ = c/a

Jumlah 3 akar: x₁.x₂.x₃ + x₁.x₂.x₄ + x₂.x₃.x₄ = – d/a

Hasil kali 4 akar: x₁.x₂.x₃.x₄ = e/a

 

Contoh Soal dan Pembahasan

1. Dari kesamaan 5x² – 2x + 14 ≡ Ax² + (B+C) x + 7 (B–C), maka A + 8B – C = ....

(A) -2

(B) 7

(C) 5

(D) 6

(E) 10

Jawab :

5x² – 2x + 14 ≡ Ax² + (B+C) x + 7 (B–C)

Jika kita pecah persamaan diatas berdasarkan sukunya

5x² = A x²          ==> A = 5

B + C = -2

7 (B – C) = 14

Setelah nilai A diketahui sebesar 5, kemudian cari nilai B dan C

7 (B – C) = 14 

   (B – C) = 2

           B  = 2 + C ...................... (pers 1)

    B + C = -2

(2 + C) + C = -2 ....................... substitusikan pers 1 atau ganti nilai B dengan (2-C)

2 + 2C = -2

      2C = (- 2) – 2

      2C = - 4

        C = -2

Untuk mencari nilai B Kembali ke pers 1

B  = 2 + C

B = 2 + (-2) = 0

# Jadi untuk A + 8B – C = 5 + 8.0 – (- 2)

                                      = 5 + 2 = 7 (B)

 

2. Suatu suku banyak f(x), jika dibagi (x–2) sisanya 5 dan dibagi (x+3) sisanya -10. Jika f(x) dibagi (x² + x – 6) sisanya adalah ....

(A)  -3x + 11

(B)  3x – 1

(C)  5x – 5

(D)  5x + 15

(E)  10x – 15

Jawab :

·         Jika f(x) dibagi (x–2) sisanya 5

Maka = P (2) = 5

·         Jika f(x) dibagi (x+3) sisanya -10

Maka = P (-3) = -10

Jika f(x) dibagi (x² + x – 6) = (x + 3)(x - 2)

P(2) : (x² + x – 6) = (x + 3) P(2)

                         = (x + 3) 5

                         = 5x + 15

P(-3) : (x² + x – 6) = P(-3) (x – 2)

                            = (-10) (x – 2)

                            = -10x + 20

Sehingga, sisa dari (x² + x – 6) untuk (x - 2) adalah 5x + 15 (D)