Volume dan Luas Permukaan Kerucut | Matematika Bangun Ruang

Hai otakers, kita lanjutkan pembahasan dari Bu Esti yang lalu yah. Setelah kalian paham bagaimana bentuk Bola dan cara menghitung luas beserta volumenya disini

Volume dan Luas Permukaan Bola.

Sesuai janji kakak di artikel sebelumnya, sekarang kita bahas lagi salah satu bentuk Bangun Ruang yaitu Kerucut. Tentu kalian sering melihat atau menjumpai benda-benda yang berbentuk seperti kerucut. Topi petani, nasi tumpeng, ataupun topi ulang tahun adalah contoh benda yang berbentuk kerucut.

Kerucut adalah bangun ruang berbentuk limas yang alasnya berbentuk lingkaran. Jika kalian perhatikan, sebuah kerucut memiliki sisi alas (bawah) yang berbentuk lingkaran. Sedangkan bagian yang membentuk sudut lancip adalah bidang lengkung yang disebut sebagai selimut kerucut. Jadi, kerucut memiliki dua buah sisi, sisi yang pertama adalah sisi alas sementara sisi yang kedua adalah sisi selimut. Lihat gambar berikut ini: 

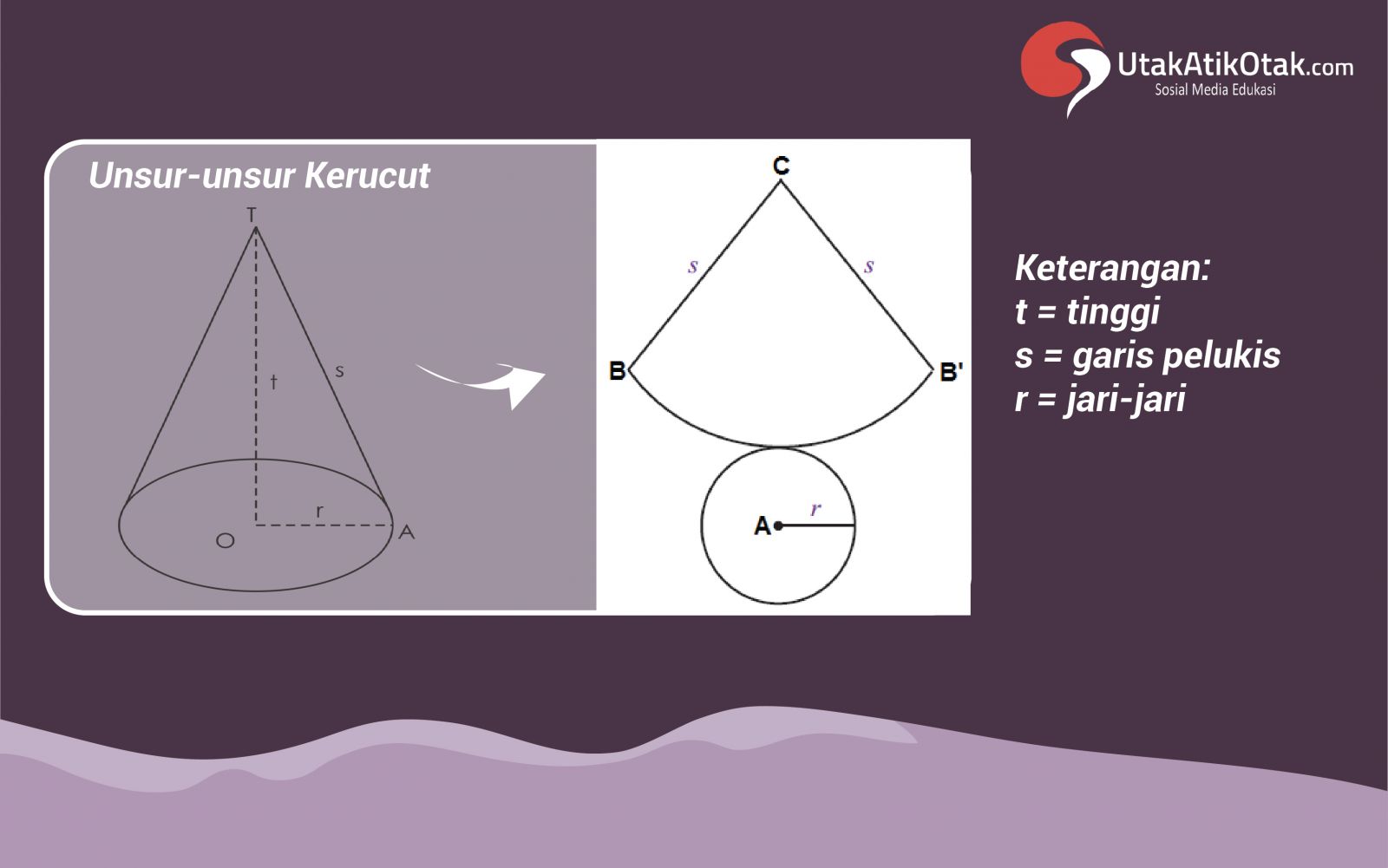
Pada gambar kerucut di atas tinggi kerucut dilambangkan dengan huruf t, huruf r merupakan jari-jari dari kerucut tersebut, sementara huruf s adalah garis pelukis.

 

Ciri-Ciri Bangun Ruang Kerucut

1. Kerucut adalah bangun ruang berbentuk limas yang alasnya berbentuk lingkaran

2. Kerucut memiliki 2 sisi,

3. Kerucut memiliki 1 rusuk,

4. Kerucut memiliki 1 titik puncak,

5. Kerucut memiliki Jaring-jaring kerucut yaitu lingkaran dan segitiga.

Apabila sebuah kerucut dipotong dengan mengikuti garis pelukisnya, maka akan terbentuk sebuah jaring-jaring kerucut seperti ini:

 

 

Rumus Bangun Ruang Kerucut

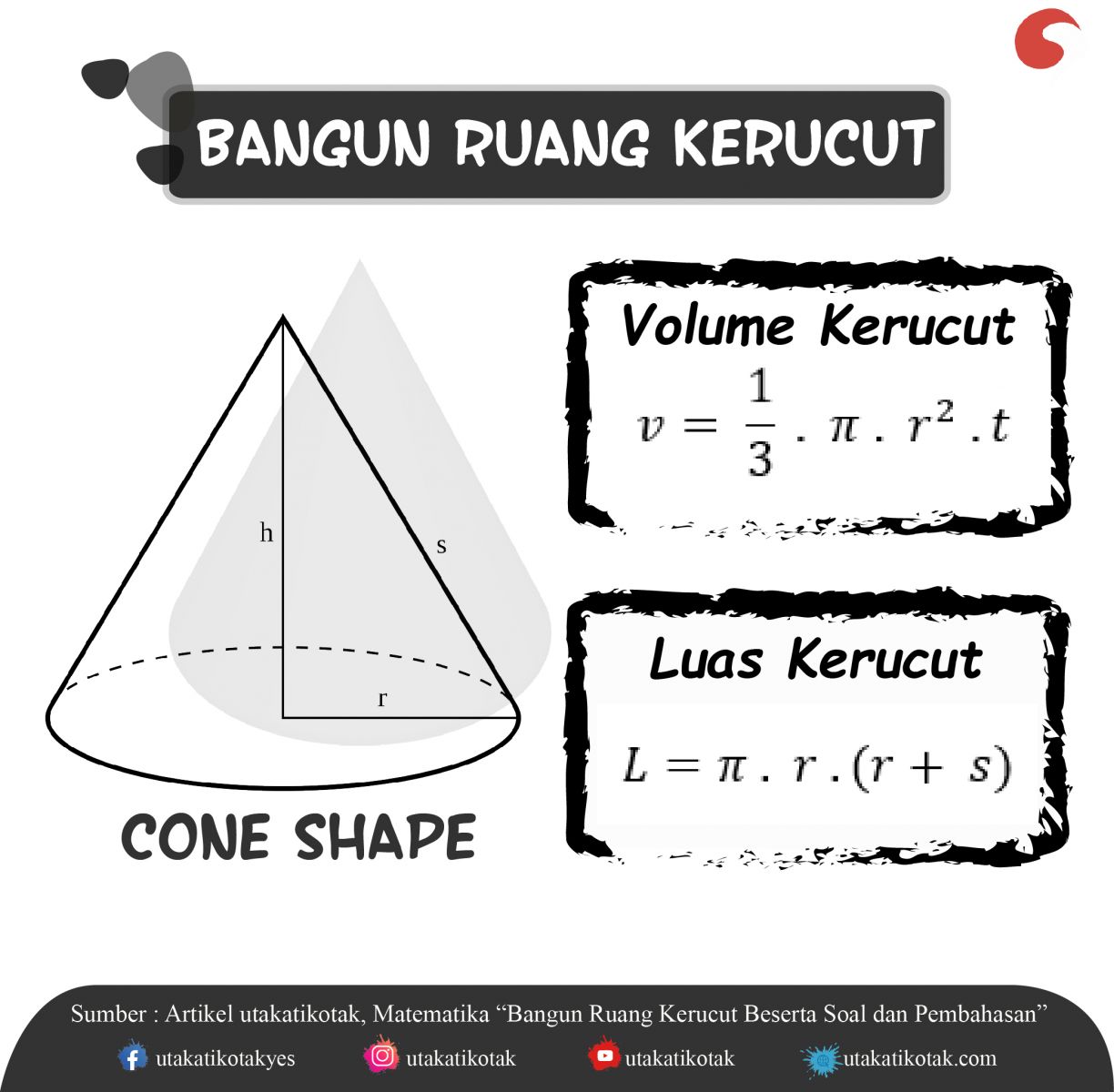
Volume Kerucut

V =  ¹/₃πr² t

Luas kerucut  = luas alas + luas selimut

• Luas alas kerucut = luas lingkaran = π x r x r = πr²

• Luas selimut kerucut = π x r x s

Luas kerucut  = luas alas + luas selimut

= (π x r x r) + (π x r x s)

= π x r ( r + s )

Luas Kerucut = luas alas + luas selimut atau

L = π x r ( r + s )

Soal Bangun Ruang Kerucut

1. Jika diameter kerucut I adalah 2 kali diameter kerucut II, tinggi kerucut I adalah sama dengan tinggi kerucut II. perbandingan volume kerucut I dan volume kerucut II adalah...

Jawab : perbandingan volume kerucut I dan volume kerucut II adalah 2 : 1

2. Sebuah kerucut tingginya 15 cm jika volume kerucut tersebut 6.930 cm kubik maka diameter kerucut kerucut tersebut

Jawab: 

V =  ¹/₃πr² t

6930 = 1/3 x 22/7 x r² x 15

6930 = 110/7 x r²

r² = 6930 x 7/110

r² = 441

r = 21

diameter = 2 x r = 2 x 21 = 42
Jadi diameter kerucut yaitu 42 cm

3. Sebuah kerucut memiliki jari jari 10cm dan tinggi 24cm tentukanlah:panjang garis pelukis kerucut,volume kerucut,luas selimut kerucut,dan luas seluruh kerucut

Jawab:

Dari soal diatas diketahui bahwa:

Jari-jari kerucut = r = 10 cm

Tinggi kerucut = t = 24

Maka,

Panjang garis pelukis kerucut = s = ?

s = √t² + r²

       = √24² + 10²

       = √576 + 100

       = √676

       = 26 cm

Volume kerucut = v =?

v = 1/3 x π x r² x t

  = 1/3 x 3,14 x 10 cm x 10 cm x 24 cm  

  = 2.512 cm³

Luas selimut kerucut = πrs

                                   = 3,14 x 10 x  26

                                   =  816,4 cm²          

Luas seluruh kerucut

  = π x r ( r + s )

  = 3,14 x 10 cm ( 10 cm + 26 cm )

  = 31,4 cm x 36 cm

  = 1130,4 cm²

4. Jika panjang jari jari kerucut A adalah 2 kali panjang jari jari kerucut B dan tinggi kerucut A sama dengan tinggi kerucut B, berapakah volume kerucut A dengan volume kerucut B??

Jawab:

dimana A=1 dan B=2

r₁=2r₂      

t₁=t₂

Volume Kerucut(1)=1/3 π r₁² t₁ .........(1)

Volume Kerucut (2) = 1/3 π r₂² t₂ .......(2)

substitusi r₁=2r₂ dan t₁=t₂ ke persamaan (1) diperoleh

Volume Kerucut (1) = 1/3 π (2r₂)²  t₂

                            = 1/3 π  4 r₂²  t₂

                            = 4 (1/3 π  r₂²  t₂)

                            = 4 Volume Kerucut (2)
Jadi Volume Kerucut A menjadi 4 kali Volume Kerucut B

5. Sebuah kerucut benda padat terdapat rongga ditengah yang berbentuk kerucut pula. Diameter kerucut 8 cm sedangkan diameter rongga kerucut sama dengan 1/2 diameter kerucut luar. Garis pelukis kerucut luar 10 cm. Tinggi kerucut rongga sama dengan 2/3 tinggi kerucut luar. Hitunglah
a. volume kerucut rongga
b. selisih antara kerucut luar dengan kerucut rongga

Jawab:

Ukuran kerucut luar:

r₁ = ½ diameter = ½ (8) = 4 cm

s₁ = 10 cm

t₁ = √(10² – 4²) = √(100 – 16) = √84 = 9,165 cm

Ukuran kerucut rongga:

d₂ = ½ diameter kerucut luar = ½ (8) = 4 cm

r₂ = ½ d₂ = ½ (4) = 2 cm

t₂ = 2/3 t₁= 2/3 (9,165) = 6,11 cm

a. Volume kerucut rongga = V₂

V₂ = 1/3 π r₂² t₂

      = 1/3 (3,14) (2)² (6,11)

      = 25,58 cm³

b. Yang ditanyakan selisih apa nih?

Jika yang ditanyakan selisih volume, hitung dulu volume kerucut luar (V₁), maka selisihnya adalah 

V₁ – V₂.

Nahh itu tadi pembahasan tentang Volume dan Luas permukaan Kerucut yah otakers. Nantikan pembahasan bangun ruang selanjutnya disini ya. Sampai Jumpa!