Turunan Fungsi Aljabar

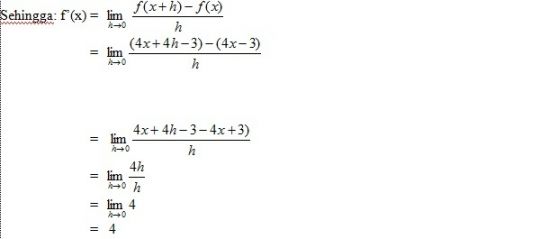
Turunan fungsi (diferensial) adalah fungsi lain dari fungsi sebelumnya. Contohnya fungsi f menjadi f’ yang mempunyai nilai tidak beraturan. Turunan fungsi digunakan untuk menyelesaikan berbagai masalah dalam geometri dan mekanika.

Aturan - aturan dalam turunan fungsi:

    f(x), maka f'(x) = 0
    Jika f(x) = x, maka f’(x) = 1
    Aturan pangkat: Jika f(x) = xn, maka f’(x) = n X n - 1
    Aturan kelipatan konstanta: (kf) (x) = k. f’(x)
    Aturan rantai: (f o g) (x) = f’ (g (x)). g’(x))

 

Contoh:

Tentukan turunan dari f(x) = 4x - 3

Jawab:

f(x) = 4x - 3

f(x + h) = 4(x + h) - 3

= 4x + 4h -3
 

Turunan jumlah, selisih, hasil kali dan hasil bagi kedua fungsi

1. Turunan f(x) = axn adalah f’(x) = anxn-1 atau dy/dx = anxn-1

2. Untuk u dan v suatu fungsi,c bilangan Real dan n bilangan Rasional berlaku

a. y = ± v →y’= v’±u’

b. y = c.u →y’= c.u’

c. y = u.v →y’= u’v + u.v’

e. y = un →y’= n. un-1.u’

Contoh:

1. Jika f(x) = 3x2 + 4 maka nilai f1(x) yang mungkin adalah ....

Jawab:

f(x) = 3x2 + 4

f1(x) = 3.2x

= 6x

2. Turunan pertama dari f(x) = (3x2 - 6x) (x + 2) adalah ...

Jawab:

f(x) = (3x2 - 6x) (x + 2)

Cara 1:

Misal: U = 3x2 - 6x

U1 = 6x - 6

V = x + 2

V1 = 1

Sehingga:

f’(x) = U’ V + U V’

f1(x) = (6x - 6)(x+2) + (3x2+6x).1

f1(x) = 6x2 + 12x - 6x - 12 + 3x2 - 6x

f1(x) = 9x2 - 12

Cara 2:

f(x) = (3x2 - 6x) (x + 2)

f1(x) = 3x-3+6x2 - 6x3 - 12x

f1(x) = 9x2+12x -12x - 12

f1(x) = 9x2 - 12