Soal Bilangan Berpangkat Bulat Positif, Negatif dan Nol

Otakers !

Kalian tentu sudah mempelajari beberapa bentuk operasi hitung bilangan bulat matematika diantaranya penjumlahan, pengurangan dan perkalian bukan?

Nahh selanjutnya kalian akan dikenalkan materi dan soal operasi hitung lainnya yaitu terkait bilangan berpangkat dan bentuk akar. Namun dalam artikel ini, kita hanya akan membahas Bilangan Berpangkat. Tapi sebelum mengenal lebih lanjut tentang bilangan berpangkat, kalian harus tahu dulu apa itu bilangan berpangkat.

Pengertian Bilangan Berpangkat

“Perpangkatan merupakan perkalian berulang dari suatu bilangan yang sama. Bilangan pokok yang dikalikan berulang tersebut dikenal dengan sebutan ‘basis’, sementara banyaknya bilangan pokok yang digunakan dalam perkalian berulang tersebut dikenal dengan sebutan ‘pangkat’ atau ‘eksponen’.

Contoh :

4 x 4 x 4 x 4 x 4 x 4 = 4⁵

Cara membacanya yaitu Empat pangkat lima

4⁵  adalah bentuk bilangan berpangkat, dengan 4 sebagai ‘basis’ dan 5 sebagai ‘pangkat atau eksponen’.

Sehingga didapatkan rumus bilangan berpangkat seperti di bawah ini

Pangkat diatas berfungsi untuk menentukan jumlah faktor yang di ulang.

a × a × a × a … sebanyak n = aⁿ

Ada beberapa jenis bilangan berpangkat yaitu diantaranya bilangan berpangkat positif (+), bilangan berpangkat negatif (-) dan bilangan berpangkat nol (0).

1. Bilangan Berpangkat Positif

Bilangan berpangkat positif adalah bilangan yang memiliki pangkat atau eksponen positif. Bentuk dari bilangan berpangkat positif dapat didefinisikan seperti gambar di bawah ini ya

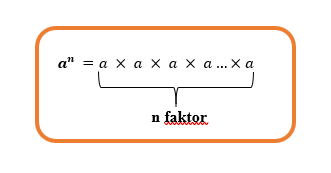
Keterangan :

a = bilangan pokok/basis, yang dalam hal ini berupa bilangan real

n = eksponen/pangkat, yang berupa bilangan positif

Oh iya otakers, bilangan berpangkat positif juga memiliki beberapa sifat lho diantaranya

a^m x aⁿ = a^m+n

a^m : aⁿ = a^{m-n ,} untuk m>n dan b ≠ 0

(a^m)ⁿ = a^mn

(ab)^m = a^m b^m

(a/b)^m = a^m/b^m , untuk b ≠ 0

Nahh, untuk pembahasan sifat-sifat tersebut kalian simak uraian di bawah ini ya otakers

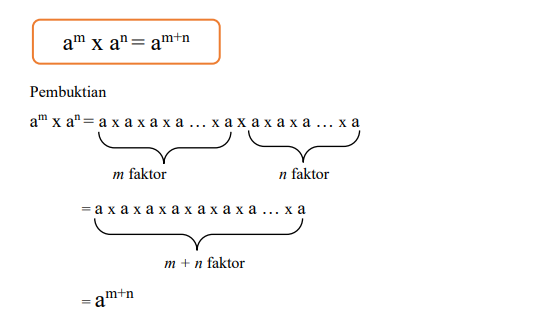
Contoh :

5² x 5⁴ = (5 x 5) x (5 x 5 x 5 x 5)

           = 5²⁺⁴

                 = 5⁶

Baca Juga :

Bilangan Berpangkat : Sifat-Sifat dan Contoh Soal

Contoh Soal Bilangan Berpangkat beserta Jawaban

Contoh Soal Bilangan Berpangkat dan Pembahasannya

 

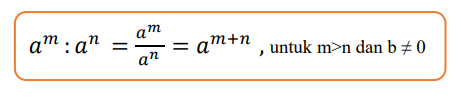
Jadi, untuk sifat ini jika kalian harus melakukan operasi pembagian bilangan berpangkat dengan nilai basis sama dan eksponen/ pangkat berbeda maka caranya kalian cukup mengurangi pangkatnya saja.

Contoh :

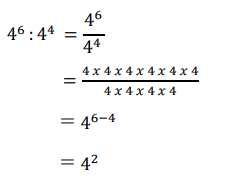
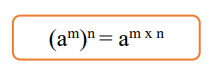
Sifat berpangkat selanjutnya yaitu bilangan berpangkat yang dipangkatkan Kembali. Jika kalian belum paham pasti menyangka ini ribet banget ya. Otakers kalian ga perlu bingung ya, jika kalian menemui soal dengan sifat seperti ini kalian hanya perlu mengalikan pangkat dari yang pertama dengan pangkat yang kedua.

Contoh :

(8³)² = 8³ x 8³

        = (8 x 8 x 8) x (8 x 8 x 8)

        = 8^3x2

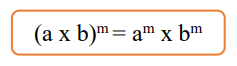
Sifat berpangkat satu ini berkaitan dengan operasi perkalian terhadap kelompok bilangan. Nahh, supaya nggak sulit kalian perlu memecah kelompok bilangan yang berada di dalam tanda kurung dan menjadikan masing-masing bilangan sebagai basis dengan eksponen yang sama.

Contoh :

(7 x 5)³ = (7 x 5) x (7 x 5) x (7 x 5)

            = (7 x 7 x 7) x (5 x 5 x 5)

            = 7³ x 5³

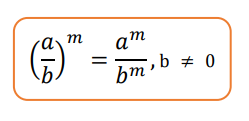
Perpangkatan terhadap pecahan bukan lagi hal yang sulit lho otakers! Berdasarkan sifat kelima ini, kamu bisa mempermudah operasi pemangkatan terhadap pecahan dengan meletakkan eksponen dalam pecahan yang dipangkatkan tersebut pada masing-masing yaitu pembilang dan penyebut.

Contoh :

Bilangan Berpangkat Negatif

Bilangan berpangkat negatif merupakan bilangan yang memiliki pangkat atau eksponen negatif (-). Adapun sifat-sifat bilangan berpangkat negatif yaitu:

Apabila suatu bilangan berpangkat aⁿ dengan a berupa Bilangan Real dan a ≠ 0, dan n ialah bilangan bulat negatif, jadi:

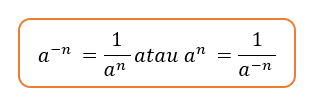
Contoh :

 Tentukan dan nyatakan dengan pangkat positif bilangan berpangkat berikut ini:

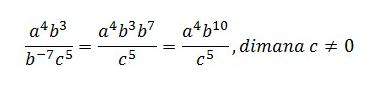
Bilangan Berpangkat Nol

Selain bilangan berpangkat positif dan bilangan berpangkat negatif, ternyata dalam dalam operasi bilangan berpangkat juga ada bilangan berpangkat nol (0). Sifat untuk bilangan berpangkat nol (0) ialah “Apabila a adalah bilangan real dan a tidak sama dengan 0, maka

Sifat ini didapat dari uraian sifat bilangan bulat positif sebelumnya yaitu

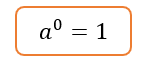
Sifat ini didapat dari uraian sifat bilangan bulat positif sebelumnya yaitu

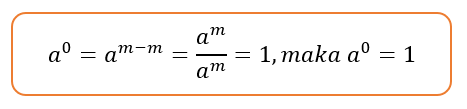
Nah, agar kalian semakin mahir dalam melakukan operasi hitung pada bilangan berpangkat dan tidak salah dalam menerapkan sifat-sifatnya, utakatikotak sudah menyiapkan beberapa contoh soal buat kalian nih.

Contoh Soal dan Pembahasan

1. 3a⁵ x 9a³ + 5a⁸

Pembahasan :

Untuk mengerjakan diatas, pertama-tama kalian harus menyelesaikan operasi perkalian terlebih dahulu dengan menggunakan sifat pertama pada bilangan berpangkat bulat positif baru kemudian melakukan operasi penambahan, sebagai berikut:

3a⁵ x 9a³ + 5a⁸  = (3 x 9 x a⁵ x a³) + 5a⁸

                         = (27 x a⁵⁺³) + 5a⁸

                         = 27 a⁸ + 5a⁸

                         = 32 a⁸

 

2. 

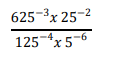
Pembahasan :

Meskipun soal ini menyajikan bilangan berpangkat bulat negatif, kalian jangan sampai terkecoh ya  otakers atau bahkan menyulitkan diri sendiri dengan menjadikan seluruh pembilang dan penyebutnya ke dalam bentuk pecahan di dalam pecahan. Kalian bisa, lho, menerapkan sifat pertama bilangan berpangkat bulat positif pada operasi perkalian yang ada di dalam soal ini. Oh iya, jangan lupa untuk menjadikan semua bilangan bulat ke dalam bentuk pemangkatannya bila memungkinkan untuk semakin memudahkan kalian menghitung, sebagai berikut:

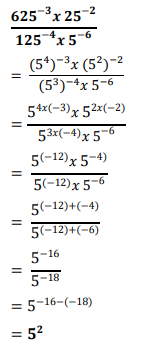
Nahh otakers, itulah pembahasan mengenai Bilangan Berpangkat Positif, Negatif dan Nol lengkap dengan contoh soal dan pembahasannya. Semangat yaa

Untuk lebih jelasnya, kalian bisa menyimak video yang ada di bawah ini ya

​​​​​