Sistem Persamaan Linear Satu Variabel

            Suatu ketika, Shinta dan Deni pergi ke toko untuk membeli beberapa alat tulis untuk perlengkapan sekolahnya. Shinta membeli 1 kotak pensil, 2 bolpoin, 3 pensil dan 2 buku tulis. Sedangkan Deni me. Dari belanjaannya Shinta harus membayar sebesar Rp 31.000, sedangkan Deni membayar Rp 13.000 untuk 3 buku dan 2 bolpoin. Setelah mereka membayar, mereka lupa meminta struk belanjaan sehingga lupa berapa harga masing” barang tersebut.

Nahh otakers, apa kalian pernah mengalami hal yang sama dengan Shinta dan Deni?

Jika jawabannya iya, maka kalian tidak perlu merasa kesulitan lagi deh karena ini mudah kok dipecahkan dengan cara matematis yaitu melalui model persamaan linear. Persamaan Linear ini banyak digunakan untuk menyelesaikan soal aplikasi matematika dalam kehidupan sehari-hari salah satu contoh seperti soal diatas.

 

Sama halnya dengan  persamaan aljabar, sistem persamaan linier juga merupakan suatu sistem hitung dalam ilmu matematika yang bisa digambarkan dalam bentuk garis lurus pada sebuah grafik. Sistem persamaan linier juga memiliki sebutan lain yaitu sistem persamaan garis.

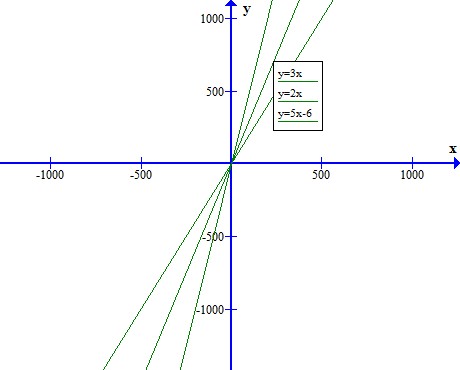
Gambar : contoh grafik persamaan linear

 

Oh iya otakers, sebelum kita membahas bagaimana cara menyelesaikan sistem persamaan linier. Apa kalian sudah memahami tentang kalimat terbuka serta definisi persamaan dan juga mengenai sistem persamaan linier itu sendiri ? Ini penting lho otakers, karena ketiga hal ini adalah bahan dasar untuk membedah materi Persamaan Linear.

1. Kalimat Terbuka

Kalimat terbuka merupakan suatu kalimat yang mempunyai variabel atau memuat variabel di dalamnya.

1. Persamaan

Persamaan merupakan suatu kalimat terbuka yang menyebutkan mengenai hubungan sama dengan (=).

1. Persamaan Linier

Persamaan persamaan linier sendiri merupakan suatu persamaan yang mana pada setiap sukunya mengandung konstanta dengan variabelnya yang berderajat satu atau tunggal.

Satu lagi nih otakers, kalian juga perlu paham apa itu variabel dan koefisien ya ...

Variabel (peubah) adalah lambang (simbol) pada kalimat terbuka yang dapat diganti oleh sembarang anggota himpunan yang telah ditentukan. Konstanta adalah lambang yang menyatakan suatu bilangan tertentu.

 

Berikut ini bentuk umum dari Persamaan Liniear

y = mx + n

Dari bentuk diatas, otakers bisa ketahui nih kalo y dan x itu termasuk variabel. Kemudian untuk m dan n termasuk kedalam konstanta.

Sistem persamaan liniear terdiri dari Persamaan Linear satu variabel, dua variabel dan lebih. Jika dikaitkan dalam kehidupan sehari-hari ini bisa dilihat dari berapa banyak jenis/ objek dari soal. Pada pembahasan kali ini kita akan mempelajari tentang Sistem Persamaan Linear Satu Variabel (SPLSV).

Persamaan linear satu variabel adalah kalimat terbuka yang dihubungkan tanda sama dengan (=) dan hanya mempunyai satu variabel berpangkat 1. 

Dalam berbagai soal persamaan linear, otakers nantinya akan diperintahkan untuk mencari Himpunan Penyelesaian baik dalam bentuk soal cerita atau langsung dalam model matematika. Himpunan Penyelesaian adalah himpunan semua pengganti dari variabel-variabel pada persamaan linear sehingga bernilai benar.

Langkah-langkah penyelesaian sistem persamaan linear satu variabel :

1. Langkah pertama adalah menyederhanakan terlebih dahulu operasi yang ada. Jika itu soal cerita, maka perlu diubah kedalam model matematika terlebih dahulu.
2. Gabungkan suku yang di dalamnya terdapat variabel ke dalam satu ruas.
3. Apabila persamaan mengandung operasi penjumlahan, maka kedua ruas harus dioperasikan dengan memakai operasi pengurangan dengan besar yang sama. Begitu juga sebaliknya.
4. Apabila persamaan mengandung operasi perkalian, maka kedua ruas harus kita operasikan dengan memakai operasi pembagian dengan besar yang sama dan bukan nol. Begitu juga sebaliknya.
5. Dahulukan operasi penjumlahan atau pengurangan terlebih dahulu sebelum melakukan pengerjaan operasi perkalian atau pembagian.

 

Contoh 1:

6x + 3 = 21, Tentukan berapa nilai x ...

Pembahasan :

6x + 3 = 21

6x + 3 – 3 = 21 – 3      => Apabila persamaan mengandung operasi penjumlahan, maka kedua ruas harus dioperasikan dengan memakai operasi pengurangan dengan besar yang sama.

6x = 18

6x / 6 = 18 / 6              => Apabila persamaan mengandung operasi perkalian, maka kedua ruas harus kita operasikan dengan memakai operasi pembagian dengan besar yang sama dan bukan nol.

X = 3

 

Contoh 2 :

5x + 4 = 6x -1, berapa penyelesaiannya?

Pembahasan :

5x + 4       = 6x -1

5x + 4 – 4 = 6x – 1 – 4

5x             = 6x – 5

5x – 6x     = 6x – 6x – 5

• x   = - 5

x   = 5

 

Contoh 3 :

Selisih dua bilangan adalah 5 dan jumlah keduanya adalah 29. Buatlah model matematikanya dan tentukan kedua bilangan tersebut.

Pembahasan :

Model matematikanya  

Bilangan I    = x

Bilangan II   = x + 5

Dan penyelesaian dari Model matematika di atas adalah

 x + ( x + 5 )     = 29

         2x + 5      = 29

         2x + 5 - 5 = 29 – 5

                2x     = 24

               2x / 2 = 24 /2

                  x     = 12

Jadi Bilangan I            = 12

        Bilangan II          = x + 5

                                    =12 + 5

                                    = 17

 

Contoh 4 :

Pak Darto ingin membuat figura berbentuk persegi panjang dengan ukuran panjang 7 cm lebih panjang dari lebarnya. Jika panjang kayu keseluruhan yang dibutuhkan sebesar 106 cm. Berapak ukuran panjang dan lebar masing-masingnya

 

Pembahasan :

Lebar     = x

Panjang = x +7

Panjang keyu yang dibutuhkan = Keliling = 106 cm

 

Keliling = 2 x ( p + l)

106 cm  = 2 x (x+7 + x)

106 cm  = 2 x ( 2x + 7 )

106 / 2   = 2 / 2 x ( 2x + 7 )

     53     = ( 2x + 7 )

53 – 7    = 2x + 7 – 7

     46     = 2x

  46 / 2   = 2x / 2

     23     = x

 

Lebar     = x = 23

Panjang

= x +7

= 23 + 7

= 30