Home » Kongkow » Materi » Sifat - Sifat Operasi Hitung Matematika

Sifat - Sifat Operasi Hitung Matematika

Oleh : UAO
- Senin, 26 Juli 2021 | 12:00 WIB
Sifat - Sifat Operasi Hitung Matematika

Ada 3 sifat yang dimiliki operasi hitung bilangan cacah. Sifat-sifat yang dimaksud adalah sifat komutatif, sifat asosiatif, dan sifat distributif.

1. Sifat distributif

Sifat distributif di dalam matematika merupakan sebuah sifat yang berhubungan dengan operasi hitung yang berlaku pada bilangan bulat. Bilangan bulat merupakan kelompok bilangan yang terdiri dari gabungan antara bilangan cacah dan bilangan negatif (....-3, -2, -1, 0, 1, 2, 3, ...).

Secara sederhana biasanya sifat distributif disebut juga sebagai sifat penyebaran, bentuk dari sifat distributif di dalam operasi hitung matematika dapat dijabarkan sebagai berikut:
 
a x (b + c) = (a x b) + (a x c)
atau
a × (b – c) = (a × b) – (a × c)
 
Ada beberapa cara yang berlaku untuk penghitungan dengan sifat distributif, perhatikan penjelasan berikut:
 
Menyatukan angka pengali
Contoh:
(2 x 4) + (2 x 6) = ...
 
Pada perhitungan di atas, angka pengali sama-sama 2 sehingga, dengan sifat distributif dapat dijabarkan menjadi seperti ini:
 
(2 x 4) + (2 x 6) = 2 x (4 + 6)
 
 
Menjumlahkan angka yang dikalikan
Contoh:
 
4 x (5 + 4) = 4 x (9) = 36
 
 
Memisahkan angka pengali
Contoh:
12 x (10 + 3) = (12 x 10) + (12 x 3)
 
 
Itulah cara-cara perhitungan yang dilakukan dengan menggunakan sifat distributif matematika.
 
2. Sifat Komutatif
Secara sederhana, sifat komutatif dapat kita artikan sebagai sifat pertukaran di dalam operasi hitung matematika
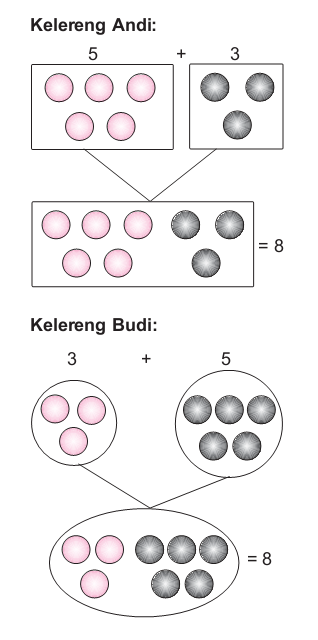
coba perhatikan perhitungan pada gambar di bawah ini:
 
Pengertian Sifat Komutatif Matematika, Contoh Soal dan Pembahasan Lengkap
 
Jadi bisa disimpulkan bahwa sifat komutatif di dalam matematika memenuhi rumus a + b = b + a dimana a dan b adalah bilangan bulat. Sifat tersebut tidak hanya berlaku pada operasi penjumlahan namun juga berlaku untuk operasi perkalian (a x b = b x a). Jadi, di  sifat komutatif matematika kita diperbolehkan melakukan pertukaran angka di dalam penjumlahan dan perkalian dengan hasil yang tetap sama.

Sifat komutatif pada operasi hitung penjumlahan

Sekarang mari kita pelajari lagi konsep sifat komutatif pada operasi hitung penjumlahan di bawah ini:
 
Contoh Soal 1
Hitunglah hasil dari 200 + 157 = ...
 
Jawab:
Hasil dari 200 + 157 = 357
 
Apabila kedua bilangan tersebut ditukar tempatnya, apakah hasilnya akan tetap sama?
 
157 + 200 = 357
 
Ternyata hasilnya tetap sama, yaitu 357. Artinya hukum komutatif berlaku untuk operasi hitung penjumlahan.
 
 

Sifat komutatif pada operasi hitung pengurangan

Sekarang mari kita coba dalam operasi hitung pengurangan.
 
200 - 157 = 43
 
Seandainya posisi bilangannya ditukar apakah hasilnya sama?
 
157 - 200 = - 43
 
Terlihat bahwa hasilnya berbeda, jika posisi bilangan itu ditukar maka hasilnya akan menjadi negatif. Artinya, sifat komutatif tidak berlaku untuk operasi hitung pengurangan (a – b ≠ b – a)

 

Baca Juga :

Sifat-Sifat Operasi Hitung Matematika

Operasi Hitung Bilangan, Urutan dan Campuran

Operasi Hitung Matematika Beserta Soal dan Pembahasan

 

Sifat komutatif pada operasi hitung perkalian

Selanjutnya, mari kita lihat penggunaan sifat tersebut di dalam operasi hitung dalam bentuk perkalian. Amati contoh soal di bawah ini:
 
Contoh Soal 2
 
Berapakah hasil dari 25 x 4 = ...
 
Jawab:
Hasil dari 25 x 4 = 100
 
Untuk menguji sifat komutatif, mari kita tukar posisinya:
 
4 x 25 = 100
 
Ternyata hasilnya pun tetap sama, artinya di dalam operasi hitung bentuk perkalian, sifat komutatif matematika dapat berlaku.
 
 

Sifat komutatif pada operasi hitung pembagian

Sekarang mari kita lihat apakah sifat ini bisa berlaku untuk operasi hitung pembagian. Kita ambil contoh pembagian di bawah ini:
 
80 : 20 = 4
 
Apabila ditukar apakah hasilnya akan sama?
 
20 : 80 = 0,25
 
Ternyata setelah posisinya ditukar hasil yang didapatkan justru berbeda. Maka dapat disimpulkan bahwa sifat komutatif tidak bisa berlaku di dalam operasi hitung pembagian (a : b ≠ b : a)
 
3. Sifat Asosiatif
Pada penjumlahan dan perkalian tiga bilangan bulat berlaku sifat asosiatif atau disebut juga sifat pengelompokan. Perhatikanlah contoh penjumlahan tiga bilangan berikut.
(2 + 3) + 4 = 5 + 4 = 9
2 + (3 + 4) = 2 + 7 = 9
Jadi, (2 + 3) + 4 = 2 + (3 + 4).
Sifat seperti ini dinamakan sifat asosiatif pada penjumlahan.
Sekarang, coba perhatikan contoh perkalian berikut.
(2 × 3) × 4 = 6 × 4 = 24
2 × (3 × 4) = 2 × 12 = 24
Jadi, (2 × 3) × 4 = 2 × (3 × 4).
Sifat ini disebut sifat asosiatif pada perkalian.
 
Sumber :
Bilangan bilangan bulat pembagian bilangan bulat perkalian bilangan bulat asosiatif distributif elemen identitas urutan operasi urutan operasi bilangan bulat soal pembahasan operasi hitung operasi hitung operasi hitung matematika sifat operasi hitung matematika operasi hitung adalah operasi hitung campuran operasi hitung pecahan operasi hitung bilangan bulat urutan operasi hitung operasi hitung campuran kelas 6 operasi hitung bilangan bulat kelas 6 operasi hitung campuran kelas 4 contoh soal sifat-sifat operasi hitung sifat sifat operasi hitung yang berlaku pada perkalian bilangan bulat adalah sifat asosiatif contoh soal sifat komutatif asosiatif dan distributif operasi hitung campuran kelas 4 operasi hitung adalah soal operasi hitung campuran kelas 4 sifat distributif kelas 5

Artikel Terkait

Kuis Terkait

Video Terkait

Cari Artikel Lainnya