Rumus Jaring Jaring Balok Dan Cara Membuatnya

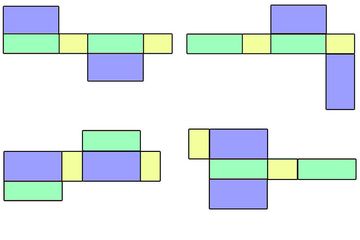
Balok adalah bangun ruang yang merupakan gabungan antara beberapa persegi dan persegi panjang.

Balok memiliki ciri-ciri :

- Memiliki 12 rusuk

- 8 titik sudut

- Terdiri dari 6 sisi

- Seluruh sudutnya pasti berbentuk siku-siku;

- Mempunyai 12 diagonal bidang dan 4 diagonal dalam bentuk bangun ruang

Jaring-jaring adalah bentuk asli dari bangun ruang yang telah dilakukan pembelahan. Atau pengertian lain dari jaring-jaring adalah sebuah bangun datar yang apabila dikaitkan akan membentuk sebuah bangun ruang.

Dari pengertian balok dan jaring-jaring diatas, maka dapat disimpulkan bahwa jaring-jaring balok adalah hasil berupa satuan bangun yang merupakan pembelahan dari bangun ruang berupa balok.

Baca juga: Rumus Bangun Ruang: Kubus, Balok, Tabung, Bola dll Beserta Gambar

Rumus Jaring Jaring Balok

d1= √ (p2 + l2)

d2= √ (p2 + t2)

d3= √ (l2 + t2)

dr= √ (p2 + l2+ t2)

Ls= 2 (p + l )t Lp= 2 (pl + pt + lt) V = plt

dengan:
p = panjang balok
l = lebar balok
t = tinggi balok
d1 = panjang diagonal sisi alas/ atas
d2 = panjang diagonal sisi depan/ belakang
d3 = panjang diagonal sisi samping kiri/ kanan
dr = panjang diagonal ruang balok
Ls = luas selimut/ selubung balok
Lp = luas permukaan balok
V = volume/ isi balok

Cara Membuat Jaring-jaring Balok

Untuk lebih memantapkan pemahaman tentang jaring-jaring balok, kita akan mencoba praktek membuat jaring-jaring balok.

Jaring Jaring Balok 12

Ambil sebuah kardus yang berbentuk balok

Jaring Jaring Balok 13

Gunting kardus sesuai pola dari kubus pada titik-titik tertentu. Jangan sampai sisakan satu sisi bawah dan satu sisi samping.

Jaring Jaring Balok 14

Maka akan kamu dapatkan bentuk berupa jaring-jaring balok seperti gambar di atas.

Setelah kita membelah kotak kardus menjadi sebuah jaring-jaring balok, maka dapat kita ketahui bahwa jaring-jaring balok tersusun dari 6 buah persegi panjang yang terdiri dari 3 persegi panjang yang sama besar. Maka

Persegi panjang ABCD sama dengan EFGH.
Persegi panjang EHDA sama dengan BCGF.
Persegi panjang ABFE sama dengan DCGH.