Program Linier Dua Variabel Beserta Contoh Soal

Program linear merupakan salah satu metode dalam menentukan solusi optimal dari suatu permasalahan linear.

Berikut merupakan langkah-langkah dalam melakukan optimasi menggunakan teknik program linear.

1. Tentukan variabel-variabel kendalanya.
2. Tentukan fungsi tujuan.
3. Susun model dari variabel-variabel kendala.
4. Gambarkan grafik dari model yang telah dibuat.
5. Tentukan titik-titik potong dari grafik.
6. Tentukan daerah penyelesaian yang sesuai.
7. Hitung nilai optimum dari fungsi tujuan.

Perhatikan contoh berikut ini

Contoh 1

Harga 3 baju dan 2 celana adalah R_P 270.000. Sedangkan harga 4 baju dan 1 celana dengan model yang sama adalah R_P 260.000. Tentukan model matematika yang sesuai dengan pernyataan tersebut !

Pembahasan:

* Variabel-variabel kendala
Misalkan :
x = Baju
y = Celana

* Fungsi atau persamaan dari semua variabel kendala
Fungsi 1 => 3x + 2b = R_P 270.000
Fungsi 2 => 4x + b = R_P 260.000

Sehingga didapat model matematika yang sesuai dengan pernyataan tersebut adalah

3x + 2b = R_P 270.000 dan 4x + b = R_P 260.000

Contoh 2

Dalam suatu pesawat terdapat 48 tempat duduk penumpang. Setiap penumpang kelas utama maksimum membawa 60 kg bagasi, sedangkan penumpang kelas ekonomi hanya diperbolehkan membawa bagasi maksimal 20 kg. Pesawat tersebut hanya mampu menampung total bagasi penumpang maksimum 1440 kg. Jika harga tiket penumpang kelas utama adalah Rp1.500.000,00 dan penumpang kelas ekonomi adalah Rp1.000.000,00, tentukan banyaknya tempat duduk kelas utama dan kelas ekonomi agar pendapatan dari penjualan tiket tersebut maksimum.

Pembahasan:

* Misalkan variabel-variabel kendala dimisalkan sebagai berikut.

x  : banyaknya penumpang kelas utama
y  : banyaknya penumpang kelas ekonomi

* Menentukan fungsi tujuan

Fungsi tujuan dari permasalahan tersebut yaitu menentukan pendapatan maksimum:
z = 1.500.000 x + 1.000.000 y

* Menyusun model dari variabel-variabel kendala

Fungsi 1: Banyak tempat duduk maksimum adalah 48
F: x + y ≤ 48
Fungsi 2: Banyak bagasi maksimum 60 kg (kelas utama) dan 20 kg (kelas ekonomi) dengan total bagasi maksimum 1.440 kg.
F: 60 x + 20 y ≤ 1.440

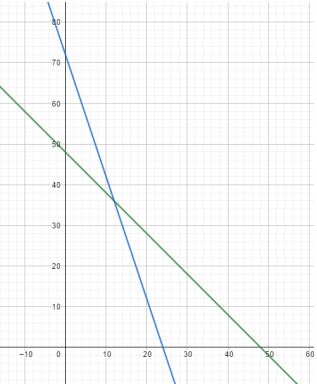
Grafik dari fungsi tersebut:

* Mencari titik potong x dan y dari masing-masing fungsi

F: x + y ≤ 48
Jika x = 0 maka :> y = 48
Jika y = 0 maka :> x = 48

F: 60 x + 20 y ≤ 1.440
Jika x = 0 maka :> y = 72
Jika y = 0 maka :> x = 24

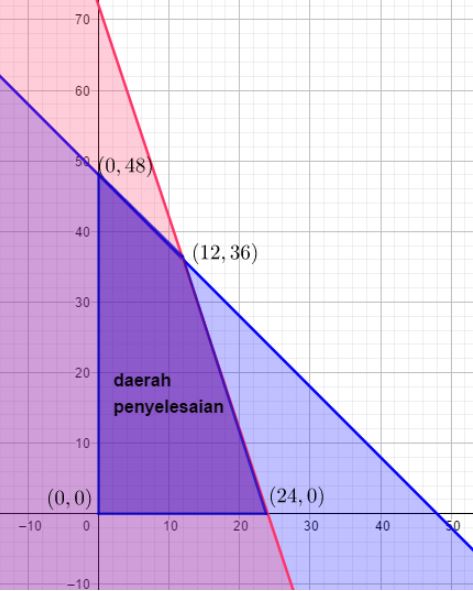
Sehingga didapatkan titik-titik yang dilalui garis yaitu (24, 0) dan (0, 72)

Gambar grafik fungsi kendala yaitu sebagai berikut.

* Menentukan titik potong kedua grafik.

Dengan menggunakan konsep SPLDV diperoleh
x + y = 48
y = 48 – x

Substitusikan nilai y pada persamaan berikut

60 x + 20 y = 1.440
Sehingga
60 x + 20 (48 – x) = 1.440
60x + 960 – 20x = 1.440
40x = 1.440 – 960
40 x = 480
x = 480/40 = 12
x + y = 48
x = 12 

Substitusikan nilai x untuk mencari nilai y
y = 48 – 12
y = 36

Titik potong kedua garis pada (12, 36)

* Menentukan daerah penyelesaian

Perhatikan daerah penyelesaian berikut.

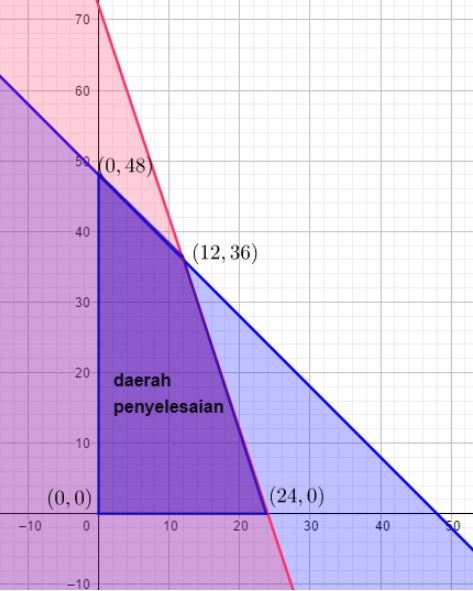
Pada gambar tersebut terdapat daerah penyelesaian yang berwarna ungu. Langkah selanjutnya yaitu menghitung nilai optimum dari fungsi tujuan.

Titik optimumnya yaitu (0, 0), (24, 0), (12, 36), dan (0, 48).

Fungsi tujuan:  z = 1.500.000 x + 1.000.000 y

Titik (0, 0)    
z = 1.500.000 (0) + 1.000.000 (0) = 0

Titik (24, 0)
z = 1.500.000 (24) + 1.000.000 (0) = 36.000.000

Titik (12, 36)
z = 1.500.000 (12) + 1.000.000 (36) = 18.000.000 + 36.000.000 = 54.000.000

Titik (0,48)
z = 1.500.000 (0) + 1.000.000 (48) = 48.000.000

Sehingga didapatkan maksimum penjualan tiket yaitu 54.000.000

Jadi, agar penjualan tiket maksimum maka banyaknya penumpang kelas utama adalah 12 penumpang dan banyaknya penumpang kelas ekonomi adalah 36 penumpang.