Operasi Penjumlahan dan Pengurangan Bilangan Bulat
.jpg)
Sebelum kita membahas bentuk operasi penjumlahan dan pengurangan bilangan bulat, otakers perlu memahami terlebih dahulu nih apa itu bilangan bulat
Bilangan bulat merupakan suatu bilangan tak pecahan yang terdiri atas
Bilangan bulat positif : 1, 2, 3, 4, 5 . . .
Bilangan nol : 0
Bilangan bulat negatif : . . ., -5, -4, -3, -2, -1
Secara umum, himpunan bilangan bulat dituliskan sebagai { . . .,-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5}. Bilangan bulat dilambangkan dengan Z, yang berasal dari kata “zahlen” (bahasa Jerman) yang berarti bilangan.
Bilangan-bilangan bulat tersebur dapat dituliskan dan diurutkan dalam garis bilangan. Penggunaan garis bilangan saat bermanfaat saat kita melakukan operasi hitung bilangan bulat. Dalam bilangan bulat juga dapat dikelompokkan ke dalam dua bagian yaitu
Bilangan genap : . . ., -6, -4, -2, 0, 2, 4, 6, . . . Bilangan genap merupakan himpunan bilangan yang jika dibagi 2 bersisa 0.
Bilangan ganjil : . . ., -5, -3, -1, 1, 3, 5, . . . Bilangan ganjil merupakan himpunan bilangan yang jika dibagi 2 bersisa 1 atau -1.
Beberapa operasi hitung sederhana dalam bilangan bulat antara lain penjumlahan, pengurangan, perkalian, dan pembagian. Untuk pembahasan kali ini kita hanya akan fokus pada operasi penjumlahan dan pengurangan ya otakers. Dalam operasi bilangan bulat penjumlahan dan pengurangan bilangan bulat dapat disajikan dalam garis bilangan sebagai berikut.
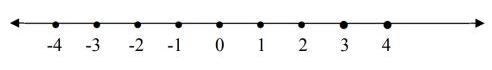
Dalam garis bilangan tersebut, terdapat bilangan bulat yang dikelompokkan bilangan bulat positif, bilangan nol dan bilangan bulat negatif.
1.Operasi Penjumlahan
Operasi penjumlahan merupakan operasi yang melibatkan tanda “ + “. Dalam garis bilangan, suatu bilangan yang dijumlahkan dengan suatu bilangan positif akan bergerak ke kanan (semakin besar). Berikut akan dijelaskan sifat-sifat dalam operasi penjumlahan.
a.Sifat Komutatif
Sifat komutatif dapat disebut sebagai sifat pertukaran. Secara umum sifat komutatif yaitu
a + b = b + a
Contoh:
3 + 9 = 9 + 3 = 12
b. Sifat Asosiatif
Sifat asosiatif ini bisa disebut juga dengan sifat pengelompokan. Secara umum sifat asosiatif dituliskan dengan
(a + b) + c = a + (b + c)
Contoh:
(5 + 6) + 2 = 5 + (6 + 2) = 13
c. Sifat identitas terhadap penjumlahan
Unsur identitas terhadap operasi penjumlahan adalah bilangan 0. Mengapa 0 dikatakan sebagai unsur identitas terhadap penjumlahan? Karena jika kita menjumlahkan suatu bilangan dengan 0, hasil operasi penjumlahan akan tetap bilangan itu sendiri. Secara umum dituliskan dengan
0 + a = a + 0
Contoh:
5 + 0 = 0 + 5 = 5
d. Unsur invers terhadap penjumlahan
Invers (lawan) dari a adalah –a.
Invers (lawan) dari –a adalah a.
Secara umum sifat invers ini dituliskan dengan
a + (-a) = 0
Contoh :
6 + (-6) = 0
e. Sifat tertutup
Penjumlahan berlaku sifat tertutup artinya penjumlahan bilangan bulat akan menghasilkan bilangan bulat juga.
Jika a dan b adalah bilangan bulat maka a + b = c dengan c merupakan bilangan bulat.
Contoh:
4 + 5 = 10
4, 5, dan 10 merupakan bilangan bulat.
2. Operasi Pengurangan
Operasi pengurangan merupakan operasi yang melibatkan tanda “ – “. Dalam garis bilangan, suatu bilangan yang dikurangi dengan suatu bilangan positif akan bergerak ke kiri (semakin kecil).
Berikut akan dijelaskan sifat-sifat dalam operasi pengurangan. Untuk suatu bilangan bulat berlaku:
a – b = a + (-b)
a – (-b) = a + b
Baca Juga:
Sifat-Sifat Operasi Hitung Matematika
Operasi Hitung Campuran Bilangan Bulat
Operasi Hitung Matematika Beserta Soal dan Pembahasan
contoh:
3 – 1 = 3 + (-1) = 2
- – (-2) = 4 + 2 = 6
a.Tidak berlaku sifat komutatif dan assosiatif
a – b ≠ b – a
(a – b) – c ≠ a – (b – c)
Contoh:
4 – 2 ≠ 2 – 4
(6 – 2) – 1 ≠ 6 – (2 – 1)
b. Pengurangan yang melibatkan bilangan 0
a – 0 = a dan 0 – a = -a
Contoh:
4 – 0 = 4 dan 0 – 4 = -4
c. Bersifat tertutup
Pengurangan yang melibatkan dua bilangan bulat, hasil operasinya juga merupakan bilangan bulat.
Jika a dan b merupakan bilangan bulat, maka a – b = c dengan c merupakan bilangan bulat.
Contoh:
7– 2 = 5.
7, 2 dan 5 merupakan bilangan bulat.
Soal Latihan Penjumlahan dan Pengurangan Bilangan Bulat
1. 692 + 207 hasilnya lebih dekat dengan ...
Jawab :
692 = 700
207 = 200
Jadi pendekatan penjumlahan kedua bilangan adalah
700 + 200 = 900
2. Angka 9, 2, 4, dan 5 akan disusun menjadi dua bilangan berbeda. Bilangan pertama disusun dari keempat angka dengan susunan dari angka terbesar ke angka terkecil. Bilangan kedua disusun dari empat angka dengan susunan dari angka terkecil ke angka terbesar. Selisih dari bilangan terbesar dengan terecil yang dihasilkan adalah ...
Jawab :
Bilangan pertama : 9.542
Bilangan kedua : 2.459
Selisih => 9.542 – 2.459 = 7.083
3. Pak Abdul mempunyai hutang pada Pak Boas sebesar Rp700.000,00. Karena anak Pak Abdul mengalami kecelakaan, Ia terpaksa meminjam uang lagi pada Pak Boas sebesar Rp200.000,00.
a. Gambarkanlah permasalahan ini pada garis bilangan
b. Tentukan berapa hutang Pak Abdul seluruhnya kepada Pak Boas.
Jawab :
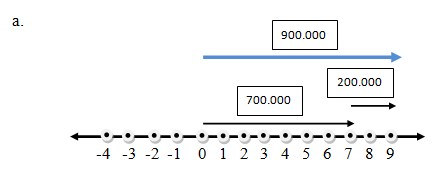
b. Jadi hutang Pak Abdul seluruhnya adalah
Hutang = Rp 700.000,00 + Rp 200.000,00
= Rp 900.000,00
4. Seorang turis di Selat Sunda melihat seekor ikan lumba-lumba meloncat sampai 4 m di atas permukaan laut. Kemudian ikan tersebut kembali ke laut menyelam sampai 9 m di bawah permukaan laut.
a. Gambarlah pada garis bilangan posisi ikan lumba-lumba dari mulai meloncat sampai menyelam lagi.
b. Tentukan selisih ketinggian meloncat dan kedalaman menyelam ikan lumba-tersebut
Jawab :
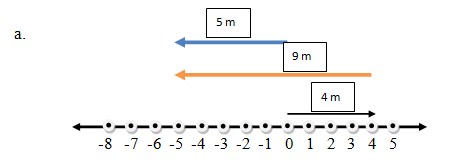
b. Jadi selisih ketinggian meloncat adalah
Selisih = 9 m – 4 m
= 5 meter
Kedalaman = 4 m – 9 m
= -5 meter dari permukaan laut
5. Tentukan hasil dari (tanpa menghitung satu persatu)
a. 1 + 3 + 5 + 7 + 9 + ... + 99
b. 1 − 2 + 3 − 4 + 5 − 6 + 7 − 8 + ... − 100
c. −100 − 99 − 98 − … − 2 − 1 − 0 + 1 + 2 + ... + 48 + 49 + 50
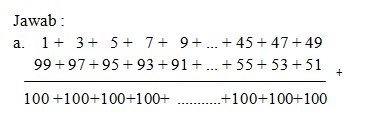
Karena antara 1 – 100 terdapat 50 angka ganjil dan 50 angka tersebut terbagi lagi menjadi 2 sehingga didapat
Jumlah keseluruhan = 100 x (50 : 2) = 100 x 25 = 2500
b. Deret bilangan terdiri dari positif ganjil dan negatif genap. Mari kita kumpulkan antara yang positif dan negatif
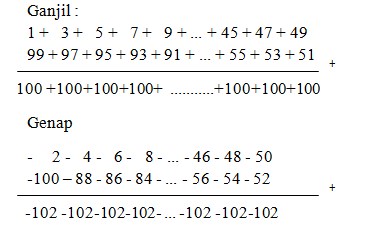
Sama dengan cara no. (a)
Untuk Jumlah keseluruhan ganjil = 100 x (50 : 2)
= 100 x 25
= 2500
Untuk Jumlah keseluruhan genap = -102 x (50 : 2)
= - 102 x 25
= - 2550
Jadi total keseluruhan = -2550 + 2500
Untuk lebih jelasnya, kalian bisa tonton penjelasan visual di bawah ini yah