Menghitung Luas Daerah Menggunakan Integral
Integral banyak sekali penggunaanya, seperti dalam menghitung luas daerah dibidang datar menggunakan integral,menghitung panjang busur, menghitung luas selimut benda putar, menghitung volume benda putar Untuk menghitung luas ini kita harus memahami apakah daerah yang dimaksud berada di atas kurva, di bawah kurva, di atas sumbu x ataupun di bawah sumbu x. Untuk itulah maka kita perlu memahami gambar kurva.
Untuk lebih jelasnya perhatikan kasus-kasus berikut
Jika kurva berada di bawah sumbu x maka metodanya adalah
Jika di antara dua kurva maka caranya sebagai berikut
Contoh soal 1
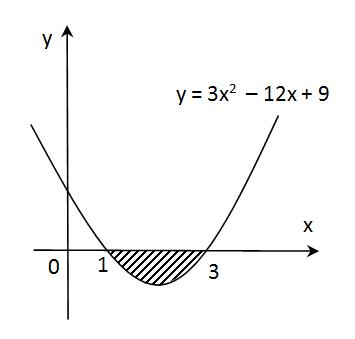
Tentukan luas daerah yang diarsir !
Contoh soal 2 :
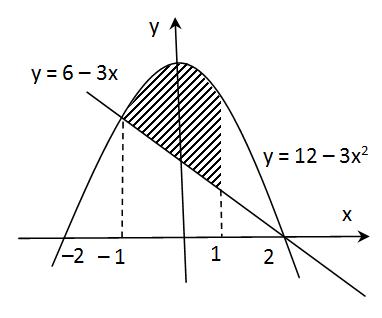
Carilah Luas daerah yang di arsir !
Jawab :
L = -33 + 6.32 – 9.3 – (-13 + 6.12 – 9.1)
L = -27 + 54 – 27 – (-1+ 6 – 9) = 0 – (-4) = 4
Baca Juga :
Tonton Video Pembahasan Soal Mencari Luas Dengan Integral Tentu
Matematika Kelas 12 | Menghitung Luas Daerah Menggunakan Integral
Memahami Dengan Mudah Integral Lipat Dua
Contoh Soal 3 :
Luas daerah yang diarsir adalah …
Jawab :
Contoh Soal 4 :
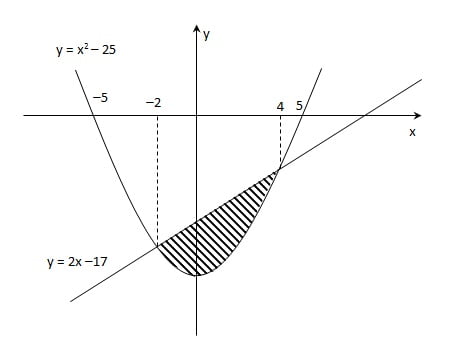
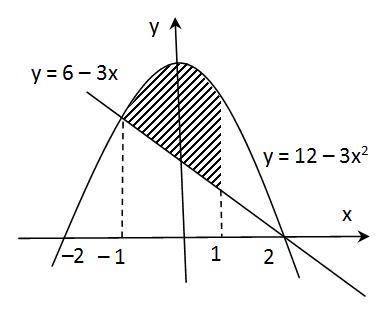
Tentukan luas daerah yang diarsir berikut
Jawab :
misalkan persamaan garis kita tulis menjadi f(x) = 2x – 17 dan parabola menjadi g(x) = x2– 25. Pada bagian yang diarsir, kurva f(x) lebih di atas dibandingkan dengan kurva g(x)
Maka luas daerah di atas bisa dinyatakan dengan
Contoh Soal 5 :
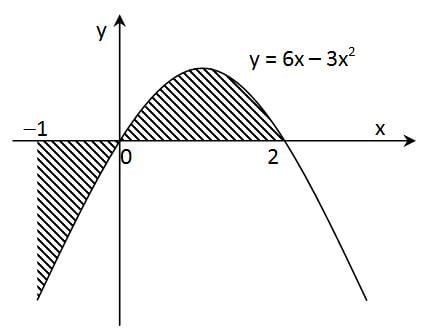
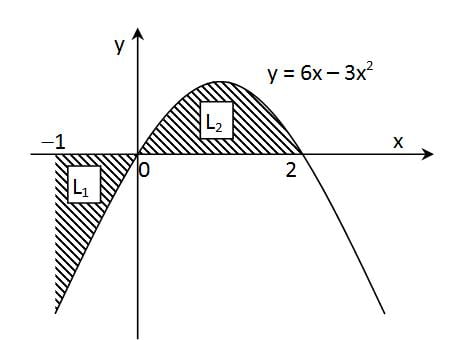
Hitunglah luas daerah yang diarsir
Jawab :
Daerah tersebut sebagian di atas sumbu x dan sebagian di bawah sumbu x. Untuk menghitung luasnya, masing-masing harus dihitung sendiri
Untuk bagian yang di bawah sumbu x, kita bisa menghitungnya sebagai berikut
L1= – 3.02 + 03 – (–3(–1)2 + (–1)3) = 0 – (–3 –1) = 4
Untuk bagian yang di atas sumbu x, kita bisa menghitungnya sebagai berikut
L2 = 3.22 – 23 – (3.02 – 03) = 12 – 8 – 0 = 4
L = L1 + L2 = 4 + 4 = 8
Baca Juga :
Memahami Dengan Mudah Integral Lipat Dua
Soal- soal dan Pembahasan Integral Tentu
Metode Menghitung Volume Benda Putar
Artikel Terkait
- Introductions (Perkenalan)
- asd
- asd
- Sinonim akulturasi adalah kontak kabudayaan #sinonim #bahasa #akulturaasi #bahasaindonesia #antonim
- Pada Suatu Pertemuan, Hadir 10 Orang yang Saling Berjabat Tangan. Banyaknya Jabat Tangan yang Terjadi Adalah... Jawaban dan Pembahasan
- Suku Kelima Suatu Barisan Aritmatika Adalah 22, Sedangkan Kesembilan Adalah 42. Suku Kelima Belas Sama Dengan... Jawaban dan Pembahasan
- Mata Uang yang Sering Digunakan Sebagai Alat Pembayaran dan Kesatuan Hitung Dalam Transaksi Ekonomi dan Keuangan Internasional Disebut...
- Kingdom yang Tidak Memiliki Dinding Sel... Jawaban dan Pembahasan
- Organel Sel yang Berperan Untuk Mendetoksifikasi Racun Adalah... Jawaban dan Pembahasan
- Diketahui Harga 4 kg Jeruk, 1 kg Semangka, dan 2 kg Apel Adalah Rp 54.000,00. Harga 1 kg Jeruk, 2 kg Semangka, dan 2 kg Apel Adalah Rp 43.000,00. Sedangkan Harga 3 kg Jeruk, 1 kg Semangka, dan 1 kg Apel Adalah Rp 37.500,00. Berapakah Harga 1 kg Semangka?