Menentukan Hubungan Antara Sudut Pusat dan Sudut Keliling
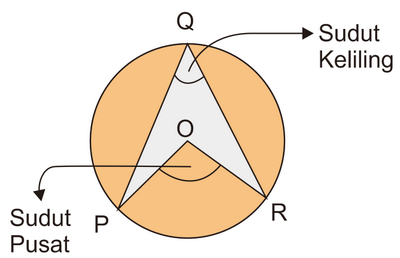
Sebelum mengetahui hubungan antara sudut pusat dengan sudut keliling, kalian perlu tau dulu pengertian dari keduanya. Perhatikan gambar di bawah ini!
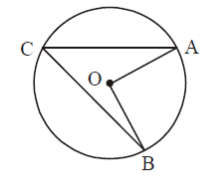
Sudut pusat adalah sudut yang titik sudutnya merupakan titik pusat lingkaran. Maka berdasarkan gambar diatas ∠AOB adalah sudut pusat lingkaran.
Selanjutnya ∠ACB dinamakan sudut keliling. Sudut Keliling adalah sudut dengan titik sudut tepat berada di lingkaran.
∠PAB dan ∠AOB menghadap busur yang sama yaitu PB.
Baca juga:
Kedudukan Antara Dua Lingkaran
Pengertian Sudut, Jenis-jenis Sudut, dan Hubungan Antar sudut
Hubungan Sudut Pusat dan Sudut Keliling
Adakah hubungan antara sudut pusat dan sudut keliling suatu lingkaran?
Jawabannya adalah ada, tetapi dengan syarat sudut pusat dan sudut keliling tersebut harus menghadap busur yang sama. Untuk mengetahui hubungan tersebut, perhatikan uraian berikut ini.
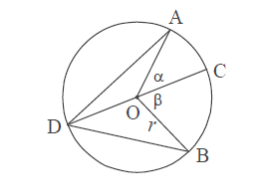
Lingkaran di atas berpusat di titik O dan mempunyai jari-jari OA = OB = OC = OD = r. Misalkan ∠AOC = α dan ∠COB = β, maka ∠ AOB = α + β.
Perhatikan ΔBOD!
∠BOD pelurus bagi ∠BOC, sehingga ∠BOD = 180° – β .
ΔBOD segitiga sama kaki, karena OB = OD = r, sehingga
∠ODB = ∠OBD = ½ (180° - ∠BOD)
Karena ∠BOD = 180° – β , maka diperoleh
∠ODB = ∠OBD = ½ (180° - (180° – β))
∠ODB = ½ β
Sekarang perhatikan ΔAOD!
∠AOD pelurus bagi ∠AOC, sehingga ∠AOD = 180° – α. ΔAOD adalah segitiga sama kaki, karena OA = OD = r, sehingga
∠ODA = ∠OAD = ½ (180° - ∠AOD)
∠ODA = ∠OAD = ½ (180° - (180° – α))
∠ODA = ∠OAD = ½ α
Dengan demikian mengunakan persamaan ∠ODB = ½β dan ∠ODA = ½α, maka besar ∠ADB dapat di cari:
∠ADB = ∠ODA + ∠ODB
∠ADB = ½ β + ½ α
∠ADB = ½ (β + α)
∠ADB = ½ ∠AOB
∠AOB = 2 x ∠ADB.
Maka dapat disimpulkan bahwa:
"Besar sudut pusat = 2 x besar sudut keliling Jika sudut pusat dan sudut keliling menghadap busur yang sama."
Contoh Soal
1. Diketahui sudut pusat ∠AOB = 65°. Tentukan besar ∠ ACB
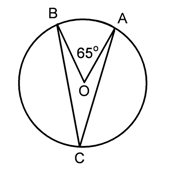
Pembahasan:
Besar sudut pusat = 2 x besar sudut keliling,
maka sudut keliling = 1/2 x Sudut Pusat
∠ ACB = 1/2 × ∠ ACB
∠ ACB = 1/2 × 65°
∠ ACB = 32,5°
2. Suatu sudut pusat Keliling dan sudut pusat menghadap busur yang mana. Jika Sudut pusat berukuran 130° maka besar sudut keliling tersebut adalah..
Pembahasan:
Besar sudut pusat = 2 x besar sudut keliling,
maka sudut keliling = 1/2 x Sudut Pusat
sehingga:
Sudut keliling = 1/2 x 130°
Sudut keliling = 65°
Credits Photo: guruspensaka.com