Matematika Rumus Bangun Ruang | Rangkuman Materi Prisma, Limas, dan Bola

Hai Otakers !

Pernahkah kalian perhatikan beberapa bagian dari rumah kalian. Kalian tentu sudah paham bentuk dan isinya bukan? Ada ruang tamu, ada ruang makan, ruang keluarga dan lain-lain. Kenapa sih kok dinamakan ruang, apa sih maksud bangun ruang itu?

Kalian pasti tidak asing lagi dengan bangun diatas ya kan, yaps itu adalah globe (bola dunia). Nahh, ini termasuk salah satu bangun ruang. Bangun ruang sendiri dapat diartikan sebagai bangunan yang secara matematika mempunyai volume atau isi. Bisa diartikan pula jika bangun ruang adalah sebuah bangun tiga dimensi yang mempunyai volume atau isi ruang serta dibatasi oleh sisi-sisi. volume atau isi sebuah bangun ruang merupakan kapasitas perhitungan ukuran banyak ruang yang bisa ditempati dalam sebuah objek. Dimana objek tersebut adalah berupa benda yang beraturan maupun yang tidak beraturan.

Nahh, kali ini kita hanya akan membahas benda yang beraturan nih karena selain bisa dihitung besar volumenya, sebuah bangun ruang juga dapat dihitung luas permukaannya. Eits, sebelum itu kalian harus paham apa itu sisi, rusuk dan titik sudut ya karena ketiga unsur diatas sangat penting lho otakers sebelum kalian mempelajari lebih jauh tentang bangun ruang.

Sisi adalah Bidang datar yang di batasi oleh rusuk dalam  suatu bangun ruang.

Rusuk adalah  ruas garis dapat berupa garis lurus atau garis lengkung pada sebuah bangun ruang.

Titik sudut adalah titik pertemuan antara 3 rusuk atau 3 sisi dalam suatu bangun ruang.

Jadi ada beberapa jenis bangun ruang yang harus kalian ketahui. Hal ini dikarenakan adanya perbedaan sifat bangun ruang tersebut satu sama lain. Yukk kita bahas satu persatu !

 

Prisma

Prisma adalah bangun ruang tiga dimensi yang dibatasi oleh alas dan tutup sama, berbentuk segi-n dan sisi-sisi tegak berbentuk persegi atau persegi panjang. Prisma segi-n memiliki n + 2 sisi, 3n rusuk dan 2n titik sudut.

Oh ya otakers, untuk bangun prisma ini terbagi menjadi beberapa bentuk, dan 3 diantaranya adalah yang sering kita dengar.

a. Kubus

Gambar : Bangun Ruang Kubus

Kubus adalah salah satu bangun prisma segi empat yang mempunyai bentuk sisi yang sama panjang. Berikut ini rumus-rumus yang bisa kalian gunakan untuk mencari unsur-unsur dari kubus.

Volume Kubus = Luas alas x t = (S x S) x S

Luas Permukaan Kubus = 6 x S

Banyak sisi Kubus (prisma segi₄) = 6

Banyak Rusuk Kubus (prisma segi₄)= 12

Banyak Titik Sudut Kubus (prisma segi₄)= 8

 

b. Balok

Gambar : Bangun Ruang Balok

Balok adalah salah satu bangun prisma segi empat yang mempunyai bentuk sisi dengan panjang rusuk berbeda (panjang, lebar, dan tinggi).

Berikut ini rumus-rumus yang bisa kalian gunakan untuk mencari unsur-unsur dari balok.

Volume Balok = Luas alas x t = (P x l) x t

Luas Permukaan Balok = 2 x ((p x l) + (p x t) + (l x t))

Banyak sisi Balok (prisma segi₄) = 6

Banyak Rusuk Balok (prisma segi₄)= 12

Banyak Titik Sudut Balok (prisma segi₄)= 8

 

c. Tabung / Silinder

Gambar : Bangun Ruang Tabung / Silinder

Tabung adalah bisa dikategorikan ke dalam prisma karena memiliki kesamaan bentuk alas dan penutup serta sisi tegak yang menglilinginya. Hanya saja pada tabung alas dan penutupnya berbentuk lingkaran.

Berikut ini rumus-rumus yang bisa kalian gunakan untuk mencari unsur-unsur dari Tabung/ silinder.

Banyak sisi Tabung = 3

Banyak Rusuk Tabung = 3

Banyak Titik Sudut Tabung = 2

 

Limas

Bangun ruang tiga dimensi yang dibatasi oleh alas berbentuk segi-n dan sisi-sisi tegak berbentuk segitiga. Limas memiliki n + 1 sisi, 2n rusuk dan n + 1 titik sudut. Perbedaan dengan prisma, limas ini tidak memiliki sisi penutup yg bentuknya sama dengan alas.

Rumus Limas

 

Nahh otakers, disini limas bisa dikategorikan menjadi beberapa bentuk tergantung dengan bentuk alasnya. Dan sebenarnya kerucut sendiri bisa digolongkan ke dalam limas lho ...

Tonton video Bangun Ruang : Volume Limas dan Kerucut

a. Limas Segitiga

Gambar : Bangun Ruang Limas Segitiga

Limas yang mempunyai alas berbentuk segitiga dengan 3 sisi tegak berbentuk segitiga. Berikut ini rumus-rumus yang bisa kalian gunakan untuk mencari unsur-unsur dari Limas Segitiga.

Banyak sisi Limas Segitiga = 4

Banyak Rusuk Limas Segitiga = 9

Banyak Titik Sudut Limas Segitiga = 4

Contoh Soal :

Diketahui sebuah Limas Segitiga memiliki alas berbentuk segitiga sama sisi dengan panjang rusuk sisi alasnya yaitu 6 cm. Sedangkan tinggi limas memiliki panjang 4 cm. Hitunglah volume dan Luas Permukaannya.

Pembahasan :

Sebelum mencari luas sisi tegak, otakers harus mencari tinggi dari sisi tegak dulu. Menggunakan rumus phytagoras.

b. Limas Segiempat

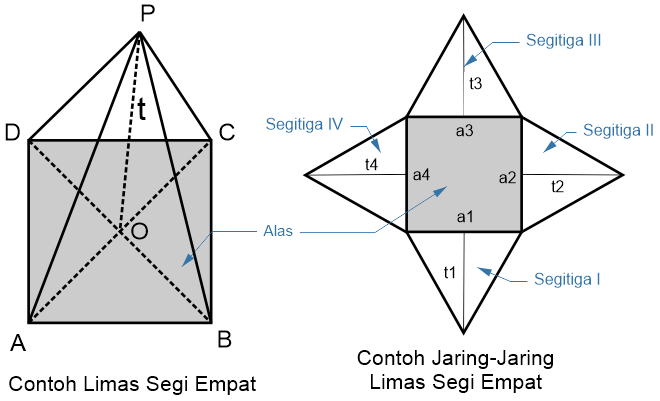
Gambar : Bangun Ruang Limas Segiempat

Limas ini mempunyai alas berbentuk segiempat dengan 4 sisi tegak berbentuk segitiga. Berikut ini rumus-rumus yang bisa kalian gunakan untuk mencari unsur-unsur dari Limas Segiempat.

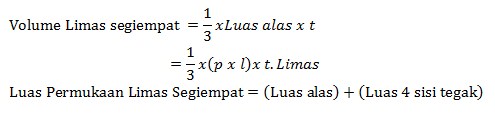
Banyak sisi Limas Segiempat = 5

Banyak Rusuk Limas Segiempat = 12

Banyak Titik Sudut Limas Segiempat = 5

 

c. Kerucut

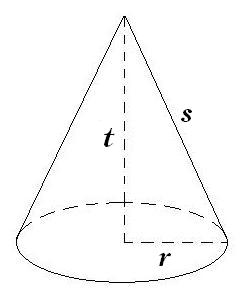
Gambar : Bangun Ruang Kerucut

Kerucut adalah sebuah limas istimewa yang beralas lingkaran. Kerucut memiliki 2 sisi dan 1 rusuk. Sisi tegak kerucut tidak berupa segitiga tapi berupa bidang miring yang disebut selimut kerucut. Berikut ini rumus-rumus yang bisa kalian gunakan untuk mencari unsur-unsur dari kerucut.

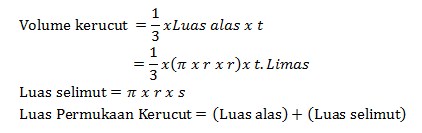
Banyak sisi Limas Kerucut = 2

Banyak Rusuk kerucut = 1

Banyak Titik Sudut Limas Segiempat = 1

Contoh Soal :

Banu memiliki kertas sebanyak 120 meter. Lalu dia ingin membuat Topi ulang tahun berbentuk kerucut dengan panjang jari-jarinya 20 cm. Jika panjang garis pelukisnya adalah 27 cm. Berapa banyak topi yang bisa dibuat oleh Banu?

 

Pembahasan :

Banyaknya kertas yang tersedia = 120 m = 12.000 cm

Luas permukaan kerucut tanpa alas (karena untuk topi, bagian alas tidak perlu dibuat

Bola

Gambar : Bangun Ruang Bola

Bola adalah bangun ruang tiga dimensi yang dibentuk oleh tak hingga lingkaran berjari-jari sama panjang dan berpusat pada satu titik yang sama. Bola hanya memiliki 1 sisi.

 

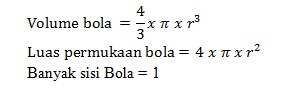
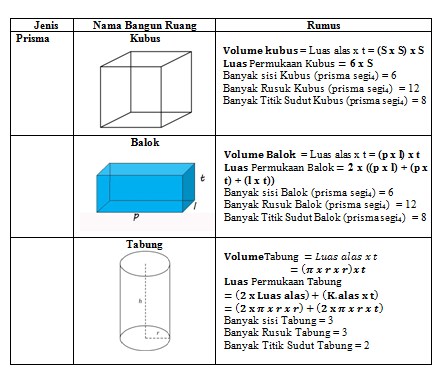
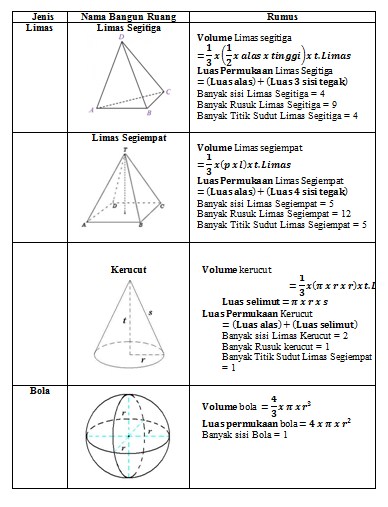
Berikut ini tabel rangkuman Rumus Bangun Ruang