Lingkaran (Unsur dan Rumus Lingkaran) | Matematika Kelas 6 SD
_Matematika_Kelas_6_SD.png)
Kita tentu pernah melihat lingkaran sebelumnya. Lingkaran memiliki bentuk yang bulat sempurna.
Setiap lingkaran memiliki titik pusat, yaitu titik yang terletak di pusat dari lingkaran itu. Lingkaran adalah sebuah bangun datar di mana jarak dari titik pusat menuju ujung lingkaran yang selalu sama.
Lengkungan – lengkungan yang terdapat dalam lingkaran saling berkaitan serta mengelilingan titik pusat dan juga membentuk daerah di dalamnya.
Tonton video selengkapnya yah!
Unsur Unsur Lingkaran Matematika
Sebuah lingkaran pastilah mempunyai beberapa bagian – bagian di dalamnya. Bagian tersebut meliputi: diameter, jari – jari, tembereng, juring, dan yang lainnya. Coba perhatikan gambar di bawah ini:
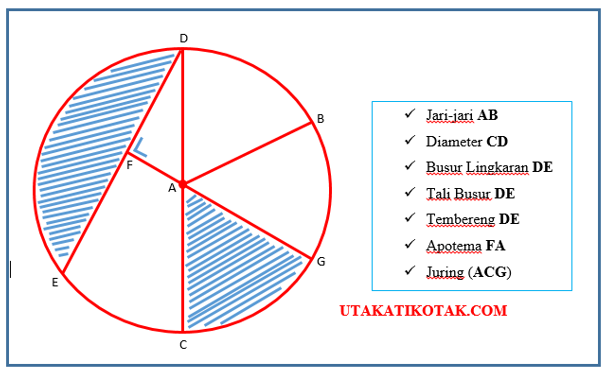
Di dalam sebuah lingkaran terdapat 8 unsur. Untuk lebih memahami dengan lebih jelas lagi tetang unsur – unsur yang terkandung di dalam lingkaran. Berikut akan kami berikan penjelasan pada masing-masing unsur – unsur yang ada di dalam lingkaran, antara lain:
1. Titik Pusat Lingkaran
Titik pusat yang terdapat dalam lingkaran merupakan suatu titik yang berada tepat ditengah – tengah lingkaran.
Pada gambar lingkaran di atas, titik pusat lingkaran terletak di huruf A.
2. Jari-jari Lingkaran
Jari – jari dalam lingkaran merupakan suatu garis yang menghubungkan antara titik pusat dengan titik pada keliling lingkaran.
Pada gambar di atas, jari – jari lingkaran berada pada garis AB, AC, AD dan juga AG.
3. Diameter Lingkaran
Yang disebut sebagai diameter pada lingkaran yaitu suatu panjang garis lurus yang mengaitkan antara dua titik pada keliling lingkaran yang melewati titik pusat lingkaran.
Dari definisi tersebut, maka dapat kita ambil kesimpulannya jika jari – jari lingkaran mempunyai nilai setengah dari diameter atau diameter mempunyai nilai dua kali dari jari – jari.
Sehingga rumus yang ditulis yaitu d = 2r.
Pada gambar di atas, diameter lingkaran atau garis tengah lingkaran berada tepat di garis CD.
4. Busur Lingkaran
Yang dimaksud dari busur pada lingkaran yaitu suatu garis lengkung yang di mana adalah bagian dari keliling lingkaran.
Busur pada lingkarang terbagi menjadi dua macam, antara lain: busur besar dan busur kecil.
Disebut sebagai busur besar apabila panjangnya lebih dari setengah lingkaran.
Sementara disebut sebagai busur kecil apabila panjangnya kurang dari setengah lingkaran. Pada gambar di atas, busur lingkarang berada di garis lengkung BC, CB, BD, dan juga BG.
5. Tali Busur Lingkaran
Yang dimaksud dari tali busur pada lingkaran yaitu garis lurus yang mengaitkan dua titik pada keliling lingkaran serta tidak melewati titik pusat lingkaran.
Apabila kita ibaratkan, tali busur lingkaran seperti halnya tali yang terdapa pada busur panah.
Pada gambar di atas, tali busur lingkaran berada pada garis DE.
6. Tembereng Lingkaran
Pengertian dari tembereng pada lingkaran yaitu daerah yang terletak di dalam lingkaran yang telah dibatasi oleh busur lingkaran serta tali busur lingkaran.
Pada gambar di atas, tembereng lingkarang telah dibatasi oleh busur DE dan juga tali busur DE.
7. Apotema Lingkaran
Unsur selenjutnya ialah Apotema Lingkaran.
Apotema lingkaran merupakan jarak terpendek antara tali busur dengan titik pusat lingkaran.
Garis apotema pada umumnya terletak tegak lurus dengan tali busur.
Pada gambar di atas, garis apotema berada di garis AF.
8. Juring Lingkaran
Yang dimaksud dengan juring pada lingkaran yaitu suatu daerah yang dibatasi oleh dua garis jari – jari serta telah dibatasi oleh sebuah busur lingkarang yang posisinya diapit oleh dua buah jari – jari tersebut.
Juring lingkarang juga terbagai menjadi dua macam. Antara lain: juring kecil dan juring besar.
Pada gambar di atas, daerah juring lingkaran berada di daerah yang diarsir yakni juring CAG.
Rumus Lingkaran Matematika
Rumus lingkaran sering kali mengecoh sebab rumus luas dan juga rumus keliling lingkaran yang sekilas terlihat hampir sama.
Beberapa rumus yang akan kita pelajari diantaranya yaitu:
-
Rumus luas lingkaran.
-
Rumus keliling lingkaran dengan jari-jari.
-
Rumus lingkaran dengan diameter.
-
Rumus diameter lingkaran.
Yuk langsung saja simak baik-baik ulasan di bawah ini.
Rumus Luas Lingkaran
Luas lingkaran dapat kita hitung dengan menggunakan rumus di bawah ini:
Luas lingkaran: π × r²
Keterangan:
-
π = phi = 3,14 atau 22/7
-
r = jari-jari, (satuan yang dipakai di mana tergantung dari soal yang dibrikan, bisa cm, dm maupun m. Serta satuan luas yaitu kuadrat atau persegi, contohnya: cm² atau m²)
Contoh Soal dan Pembahasan Luas Lingkaran
Sebuah lingkaran mempunyai jari-jari sebesar 20 cm. Hitunglah luas lingkaran tersebut?
Jawab:
Diketahui:
-
r = 20 cm
Ditanyakan:
-
Luas lingkaran?
Penyelesaian:
Luas = π × r²
= 3,14 × 400
= 1256 cm²
Sehingga, luas lingkaran tersebut yaitu 1256 cm².
Rumus Keliling Lingkaran dengan Jari-Jari
Pada waktu kita mencari keliling lingkaran, maka terdapat dua rumus yang dapat kita pakai.
Diantaranya:
Rumus pertama yang kita pakai apabila lingkaran tersebut telah diketahui diameternya.
Serta rumus kedua kita pakai dalam menghitung keliling lingkaran yang belum diketahui diameternya.
Berikut adalah pembahasan sekaligus contohnya.
Apabila diameternya tidak diketahui maka kita dapat memakai jari-jari untuk menghitung keliling lingkaran. Rumus yang digunakan ialah sebagai berikut:
Keliling ligkaran: 2 × π × r
Keterangan:
k = Keliling lingkaran
π = phi; nilainya 22/7 atau 3,14
r = jari-jari lingkaran
Contoh Soal dan Pembahasan Keliling Lingkaran dengan Jari-jari
Jari-jari lingkaran panjangnya 7 cm. Berapakah keliling linkarannya?
Jawab:
r = 7 cm
Keliling = 2 x π × r
Keliling = 2 x 22/7 × 7
K = 44 cm.
Rumus Keliling Lingkaran Dengan Diameter
Rumus ini berlaku apabila yang diketahui merupakan diameter lingkarannya. Untuk menghitung keliling dari sebuah lingkaran dengan memakai diameter, maka kita gunakan rumus sebagai berikut:
Keliling Lingkaran: k = π × d
Keterangan:
k = keliling lingkaran
π = phi =22/7 atau 3,14
d = diameter
Contoh Soal dan Pembahasan Keliling Lingkaran dengan Diamater
Tutup toples makanan diameternya 10 cm. Berapakah keliling toples tersebut?
Jawab:
d = 10 cm
Keliling = π × d
Keliling = 3,14 × 10
K = 31,4 cm.
Artikel Terkait
- Dayu Mempunyai Meja Bundar, Meja Tersebut Berdiameter 56 cm. Hitunglah Luas Meja Dayu!
- Jika Jari-jari Ban Sepeda Adalah 40 cm. Hitunglah Diameter dan Keliling Ban Sepeda Tersebut!
- Diketahui Sebuah Lingkaran Mempunyai Diameter 50 cm, Maka Berapa Luas Lingkaran Tersebut?
- Pak Andi Memiliki Sebuah Mobil yang Panjang Jari-jari Ban Mobil Tersebut Sebesar 21 cm. Jarak yang Ditempuh Mobil?
- Sebuah Roda Mempunyai Jari-jari 7,5 cm. Berapakah Keliling Roda Tersebut?