Kekongruenan dan Kesebangunan Bangun Datar

Kesebangunan Dua Bangun Datar

Dua benda dikatakan sebangun jika memiliki bentuk yang sama. Dengan memperbesar atau memperkecil suatu benda, kamu akan selalu mendapatkan benda lain yang sebangun dengan benda yang kamu miliki sebelumnya. Begitu pula sebaliknya, dua bangun yang sebangun pasti diperoleh dengan cara memperbesar atau memperkecil suatu benda yang sama.

Perhatikan gambar berikut ini

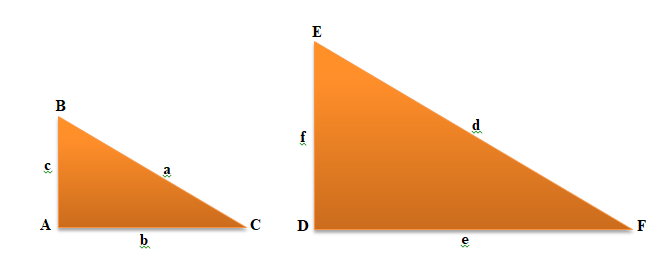
Segitiga DEF diperoleh dengan memperbesar segitiga ABC sebanyak dua kali. Pasangan-pasangan sisi a dan d, b dan e, serta c dan f disebut sisi-sisi yang bersesuaian. Jika sisi a, b, dan c panjangnya berturut-turut adalah 5 cm, 4 cm, dan 3 cm, dapatkah kamu menebak panjang sisi-sisi segitiga DEF ?

Benar, untuk memperoleh panjang sisi e, kamu cukup mengalikan panjang sisi b dengan 2. Demikian juga panjang sisi d dan f diperoleh dengan mengalikan panjang a dan c dengan 2.  Apakah kamu menyadari sesuatu? Apakah sesuatu itu terlihat seperti persamaan di bawah ini?

Dari persamaan terlihat bahwa perbandingan dari panjang sisi-sisi yang bersesuaian selalu sama, yaitu 2. Bagaimana jika bendanya tidak diperbesar dua kali tetapi tiga, empat, atau dengan bilangan lain? Apakah perbandingan panjang dari sisi-sisi yang bersesuaian tetap sama?

Jawabannya tentu saja iya, hanya saja nilainya tidak lagi 2, melainkan 3, 4, atau berapapun nilai yang kamu gunakan untuk memperbesar atau memperkecil bentuk benda yang kamu miliki mula-mula. Selain itu, sudut-sudut yang bersesuaian juga pasti sama besar.

Kita dapat dengan mudah mengatakan bahwa segitiga ABC dan DEF pada contoh di atas adalah sebangun, sebab sisi-sisi yang bersesuaian telah diletakkan bersesuaian pula. Namun pada kehidupan nyata banyak benda-benda yang sesungguhnya sebangun namun tidak terlihat kesebangunannya.

Kekongruenan dua bangun datar

Kata kongruen dapat diartikan dengan “menempati bingkainya dengan tepat” atau “dapat menutup rapat”. Dua bangun yang kongruen memiliki bentuk maupun ukuran yang sama persis. Pada bangun yang kongruen, perbandingan dari sisi-sisi yang bersesuaian selalu sama dengan satu. Bagaimana dengan sudut-sudutnya?

Tentu saja sudut yang bersesuaian juga pasti sama besar. Dalam kehidupan sehari-hari, kita bisa melihat contoh sifat kongruen pada beberapa hal, misalnya pada ubin lantai rumah, lembaran kertas pada buku catatan, dan lain sebagainya. Setiap ubin pada lantai memiliki bentuk dan ukuran yang sama persis bukan?

Kongruen dilambangkan dengan ≅, sehingga jika terdapat dua buah segitiga yang kongruen misalnya ΔABC kongruen dengan ΔDEF, maka dapat ditulis sebagai ΔABC≅ΔDEF

Dari gambar di atas diketahui bahwa ΔABC adalah segitiga sama kaki. Sisi CD merupakan garis tinggi ΔABC, sehingga membentuk ΔADC dan ΔBDC. Apakah ΔADC kongruen dengan ΔBDC?

ΔADC kongruen dengan ΔBDC (ΔADC ≅ ΔBDC) karena:

• ΔADC dapat tepat menempati ΔBDC dengan cara mencerminkan ΔADC terhadap garis CD atau semua sisi ΔADC memiliki panjang yang sama dengan ΔBDC.

• ΔABC merupakan segitiga sama kaki, sehingga ∠CAD = ∠CBD (sudut pada kaki segitiga samakaki ΔABC) dan ∠ADC = ∠BDC = 90⁰. Ini berakibat ∠ACD = ∠BCD.