Diketahui kubus ABCD.EFGH dengan rusuk 8 cm. Titik M adalah titik tengah BC. Tentukan jarak M ke EG

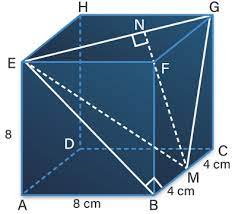
Diketahui kubus ABCD.EFGH dengan rusuk 8 cm. Titik M adalah titik tengah BC. Tentukan jarak M ke EG

Pembahasan

Soal diatas merupakan salah satu contoh untuk mencari jarak suatu titik terhadap suatu bidang. Dalam pembahasannya nanti, hal yang perlu diperhatikan adalah

• Jarak titik ke garis adalah lintasan terpendek yang menghubungkan titik dan tegak lurus terhadap garis.
• Pada segitiga siku-siku berlaku teorema Pythagoras 
• Panjang diagonal bidang pada bangun ruang kubus yang memiliki sisi a cm adalah a √2 cm

Diketahui

Kubus dengan rusuk 8 cm
Panjang diagonal bidang = 8 √2 cm
Titik M adalah titik tengah BC, maka BM = CM = 4 cm

Ditanya : Jarak M ke EG ?

Jawab 

Panjang diagonal bidang BE = EG = 8 √2 (Bisa dibuktikan dengan menggunakan rumus Phytagoras.

* Mencari panjang EM
EM = √(BE² + BM²)
EM = √(8 √2)² + 4²)
EM = √(128 + 16)
EM = √144
EM = 12 cm

* Mencari panjang MG 
MG = √(MC² + CG²)
MG = √(4² + 8²)
MG = √(16 + 64)
MG = √80
MG = √16 . √5
MG = 4√5 cm

Jika titik M tegak lurus terhadap bidang EG pada titik yang kita namakan N. Maka bisa kita bentuk segitiga EMN dan segitiga MGN. Selanjutnya kita cari panjang MN tersebut/

* Mencari panjang MN dari segitiga EMN
MN = √(EM² - EN²)
MN = √(12² - EN²)
MN = √(144 - EN²) ......... persamaan 1

* Mencari panjang MN dari segitiga MGN
MN = √(MG² - NG²)
MN = √(4√5² - (8 √2 - EN)² )
MN = √(80 - (8 √2 - EN)² ) ......... persamaan 2

Maka bisa kita hitung

MN = MN
√(144 - EN²)     = √(80 - (8 √2 - EN)² )
  144 - EN²       =     80 - (8 √2 - EN)² 
  144 - EN²       =     80 - (128 - 16 √2 EN - EN² )
  144 - EN²       =     80 - 128 + 16 √2 EN + EN²
  144                =     80 - 128 + 16 √2 EN
144 - 80 + 128 =    16 √2 EN
   192               =     16 √2 EN
    EN               =   192 / 16 √2
    EN               =   12 / √2
    EN               =   6 √2

Selanjutnya langkah terakhir mencari MN kita gunakan persamaan 1

MN = √(144 - EN²)
MN = √(144 - (6 √2)²)
MN = √(144 - 72)
MN = √(72)
MN = 6 √2 cm

Jadi jarak M ke EG adalah 6 √2 cm