Contoh Soal dan Pembahasan Akar Kuadrat Dengan Cara Pemfaktoran dan Melengkapi Kuadrat Sempurna

Mencari akar persamaan kuadrat dengan cara pemfaktoran dan melengkapi kuadrat sempurna

1. 3x² – 12 = 0

Jawab :

Pemfaktoran

Nilai, a = 3, b = 0, c = -12

maka nilai a.c = 3 x (-12) = -36

Untuk menentukan nilai p dan q, kita harus mencari dulu faktor dari hasil perkalian a dan c yaitu faktor dari (-36).

Faktor (-36) = 36, 18,12, 9, 6,4,3,2,1, -36, -18,-12,-9, -6,-4,-3,-2,-1

Kemudian pilih 2 angka dari faktor tersebut sebagai nilai p dan q yang apabila dijumlahkan menghasilkan nilai b atau 0 . Sehingga didapat nilai (-6) dan (6)

Anggap nilai p = -6 dan q = 6 .

Karena nilai a 1, maka

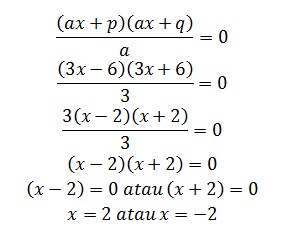
Jadi, didapat akar akar persamaan kuadrat diatas yaitu x₁ = 2 dan x₂ = -2

 

b. Melengkapi kuadrat sempurna

Kita ubah dulu persamaan untuk a=1, jadi kita bagi dengan 3 sehingga didapat

x² – 4 =0

x² – 2² =0

(x + 2) (x - 2) = 0

x = -2 atau x = 2

 

2. x² + 7x + 6 =

Jawab:

a. Pemfaktoran

Nilai, a = 1, b = 7, c = 6maka nilai a.c = 1 x 6 = 6

Untuk menentukan nilai p dan q, kita harus mencari dulu faktor dari hasil perkalian a dan c yaitu faktor dari (6).

Faktor (6) = 6,3,2,1, -6,-3,-2,-1

Kemudian pilih 2 angka dari faktor tersebut sebagai nilai p dan q yang apabila dijumlahkan menghasilkan nilai b atau 7 . Sehingga didapat nilai (1) dan (6).

Anggap nilai p = 1 dan q = 6 .

Karena nilai a =1, maka

(ax + p) (ax + q) = 0

(x + 1) (x + 6) = 0

(x + 1) = 0 atau (x + 6) = 0

x= -1 atau x = - 6

Jadi, didapat akar akar persamaan kuadrat diatas yaitu x₁ = -1 dan x₂ = -6

b. Melengkapi kuadrat sempurna

x² + 7x + 6 = 0

Menyelesaikan persamaan kuadrat dengan melengkapkan kuadrat sempurna adalah mengubah persamaan kuadrat menjadi bentuk kuadrat sempurna, yakni: (x + p)² =q

x² + 7x + 6 = 0

Sebelumnya cari angka yang akan ditambahkan lebih dulu :

Untuk angka ganjil seperti (7 x) kita harus kalikan dulu bilangan tersebut dengan setengah. Maka didapat 7/2. Lalu kuadratkan bilangan tersebut, sehingga didapatkan angka 49/4.

Kemudian :

x² + 7x + 6 = 0

x² + 7x + 49/4 = -6 + 49/4

x² + 7x + 49/4 = 25/4

(x + 7/2)² = 25/4

(x + 7/2) = (+/-) 5/2

Jadi dari hasil diatas dapat kita cari

(x + 7/2) = 5/2

x₁ = 5/2 – 7/2

     = - 2/2

     = -1

(x₂  + 7/2) =  - 5/2

x₂  = - 5/2 -7/2

= - 12/2

= - 6

 

3. -3x² – 5x + 2 = 0

Jawab:

a. Pemfaktoran

Nilai, a = -3, b = -5, c = 2 maka nilai a.c = -3 x 2 = -6

Untuk menentukan nilai p dan q, kita harus mencari dulu faktor dari hasil perkalian a dan c yaitu faktor dari (-6).

Faktor (6) = 6,3,2,1, -6,-3,-2,-1

Kemudian pilih 2 angka dari faktor tersebut sebagai nilai p dan q yang apabila dijumlahkan menghasilkan nilai b atau -5 . Sehingga didapat nilai (1) dan (6).

Anggap nilai p = 1 dan q = -6 .

Karena nilai a  tidak sama dengan 1, maka

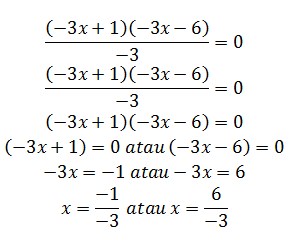
Jadi, didapat akar akar persamaan kuadrat diatas yaitu x₁ = 1/3 dan x₂ = -2

b. Melengkapi kuadrat sempurna

    3x² – 5x + 2 = 0

Menyelesaikan persamaan kuadrat dengan melengkapkan kuadrat sempurna adalah mengubah persamaan kuadrat menjadi bentuk kuadrat sempurna, yakni: (x + p)² =q

x² - 5x + 2 = 0  ==>  x² + (5/3)x – 2/3 = 0

Sebelumnya cari angka yang akan ditambahkan lebih dulu :

Kita harus kalikan dulu bilangan (5/3 x) dengan setengah. Maka didapat 5/6. Lalu kuadratkan bilangan tersebut, sehingga didapatkan angka 25/36.

Kemudian :

x² + (5/3) x – 2/3 = 0

x² + (5/3) x + 25/36 = 2/3 + 25/36

x² + (5/3) x + 25/36  = 49/36

(x + 5/6)² =49/36

(x + 5/6) = 7/6

Jadi dari hasil diatas dapat kita cari

(x + 5/6) = 7/6

x₁ = 7/6 – 5/6

x₁ = 2/6

= 1/3

(x + 5/6) = - 7/6

x₂  = - 7/6 - 5/6

= - 12/6

= - 2

Untuk lebih jelasnya, lihat video di bawah ini ya otakers ...