Cara Mudah Menentukan Rumus Suku Ke-n Barisan Aritmatika

Cara mencari suku ke-n dari barisan aritmatika ini sangat perlu anda pahami secara konsep karena materi ini sendiri akan dijumpai lagi pada tingkat SMA/MA.

Dalam barisan aritmatika ini kita akan mengenal tingkatan-tingkatan barisan aritmatika. Mulai dari barisan aritmatika tingkat kesatu, kedua, ketiga, dan tingkat seterusnya. Dalam hal ini kita hanya akan membahas sampai barisan aritmatika tingkat ketiga. Adapun rumus secara umum suku ke-n dari barisan artimatika ialah :

Tingkat 1 => Un = an + b
Tingkat 2 => Un = an² + bn + c
Tingkat 3 => Un = an³ + bn² + cn + d

Barisan Aritmatika Tingkat Kesatu

Contoh barisan aritmatika tingkat ke-1 yaitu sebagai berikut :

a. 2, 4, 6, 8, 10, . . .
b. 3, 6, 9, 12, 15, . . .

Kenapa disebut barisan aritmatika tingkat kesatu ? Hal ini karena selisih 2 suku yang berdekatan memiliki nilai sama berada pada tingkat pertama. Dan perhatikan gambar di bawah ini :

Adapun untuk mencari rumus ke-n dari barisan aritmatika tingkat kesatu, silahkan perhatikan uraian berikut. Kita ketahui bahwa rumus umum untuk mencari suku ke-n dari barisan aritmatika tingkat kesatu yaitu :

Un = an + b
maka:
U1 = a + b
U2 = 2a + b
U3 = 3a + b
U4 = 4a + b

Dan jika dibuat dalam barisan aritmatika maka akan tampak seperti berikut ini :

Dari gambar di atas terlihat bahwa selisih antara U2 dengan U1, U3 dengan U2, dan U4 dengan U3 adalah a.

Contoh Soal 1

Tentukanlah rumus suku ke-n dari barisan aritmatika 6, 9, 12, 15, 18, . . .

Penyelesaian:

Dari gambar di atas maka :

a = 3

a + b = 6
3 + b = 6
b = 3

Un = an + b
Un = 3n + 3

Jadi, rumus suku ke-n dari barisan aritmatika 6, 9, 12, 15, 18, . . . ialah Un = 3n + 3

Barisan Aritmatika Tingkat Kedua

Contoh dari barisan aritmatika tingkat kedua ialah sebagai berikut :

a. 1, 3, 7, 13, 21, . . .
b. 5, 6, 10, 17, 27, . . .
c. 4, 6, 13, 25, 42, . . .

Selisih dari kedua suku yang berdekatan yang bernilai sama berada pada tingkatan yang kedua. Perhatikanlah gambar di bawah ini :

Untuk mencari suku ke-n dari barisan aritmatika tingkat ke-2 ini, silahkan perhatikan uraian berikut ini :

Un = an² + bn + c
U1 = a(1)² + b(1) + c = a + b + c
U2 = a(2)² + b(2) + c = 4a + 2b + c
U3 = a(3)² + b(3) + c = 9a + 3b + c
U4 = a(4)² + b(4) + c = 16a + 4b + c

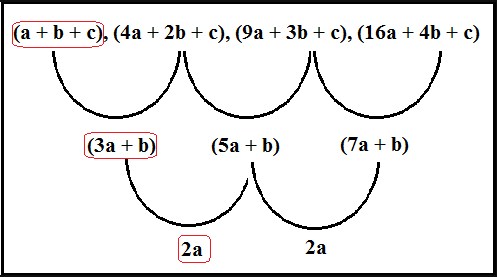
Jika dibuat dalam bentuk barisan maka akan tampak seperti berikut ini :

Dengan menggunakan barisan bertingkat maka barisan aritmatika 1, 3, 7, 13, 21, . . . akan diperoleh seperti berikut ini :

Maka:

a + b + c = 1
3a + b = 2
2a = 2

Dengan metode substitusi maka akan diperoleh:

a = 1, b = – 1 dan c = 1 maka
Un = an² + bn + c
Un = 1n² + (– 1)n + 1
Un = n² – n + 1

Maka, rumus untuk menentukan nilai a, b, dan c pada barisan aritmatika tingkat ke-2 yaitu :

a + b + c = U1
3a + b = U_t1
2a = U_t2

Contoh Soal 2

Tentukanlah rumus suku ke-n dari barisan aritmatika 4, 6, 13, 25, 42, . . .

Penyelsaian:

2a = 5
a = 5/2

3a + b = 2
3(5/2) + b = 2
15/2 + b = 2
b = 4/2 – 15/2
b = – 11/2

a + b + c = 4
5/2 – 11/2 + c = 8/2
c = 8/2 – 5/2 + 11/2
c = 14/2

Un = an² + bn + c
Un = (5/2)n² – (11/2)n + 14/2
Un = ½ (5n² – 11n + 14)

Barisan Aritmatika Tingkat Ketiga

Contoh dari barisan aritmatika tingkat 3 ialah sebagai berikut :

a. 1, 3, 7, 15, 29, . . .
b. 1, 2, 4, 10, 23, . . .

Selisih antara dua suku yang berdekatan memiliki nilai sama berada pada tingkatan yang ketiga. Perhatikanlah gambar di bawah ini :

Dengan cara yang sama seperti mencari rumus suku ke-n aritmatika tingkat kedua, maka akan diperoleh rumus untuk mencari a, b, c dan d yaitu:

a + b + c + d = U1
7a + 3b + c = U_t1
12a + 2b = U_t2
6a = U_t3

Contoh Soal 3

Tentukanlah rumus suku ke-n dari barisan aritmatika 1, 3, 7, 15, 29, . . .

Penyelesaian:

6a = 2
a = 1/3

12a + 2b = 2
4 + b = 2
b = – 2

7a + 3b + c = 2
7/3 – 6 + c = 2
c = 6/3 + 18/3 – 7/3
c = 17/3

a + b + c + d = 1
1/3 – 2 + 17/3 + d = 1
d = 3/3 – 1/3 + 6/3 – 17/3
d = – 9/3 = – 3

Un = (1/3)n³ – 2n² + (17/3)n – 3
Un = (1/3)(n³ – 6n² + 17n – 9)