Barisan dan Deret Geometri Beserta Soal

A. Barisan Geometri
Barisan geometri adalah baris yang nilai setiap sukunya didapatkan dari suku sebelumnya melalui perkalian dengan suatu bilangan r. Perbandingan atau rasio antara nilai suku dengan nilai suku sebelumnya yang berdekatan selalu sama yaitu r.
Sehingga untuk mencari nilai r bisa dengan menggunakan rumus:
r = Un / Un-1
Rumus suku ke-n Barisan Geometri
Barisan geometri ini adalah baris yang nilai setiap sukunya didapatkan dari suku sebelumnya melalui perkalian dengan suatu bilangan. Jadi dapat dikatakan jika pada aritmatika berbeda melalui penambahan dan pengurangan, sementara barisan geometri melalui perkalian. Rumusnya tentu juga berbeda yah!
Un = a.r (n-1)
Simbol-simbol di sini sama seperti penjelasan yang di rumus suku ke-n barisan aritmatika. Simbol Un di sini menunjukkan suku ke-n, sementara simbol a menunjukkan suku pertama atau awal dari barisan. Sedangkan simbol r melambangkan perbandingan atau rasio antara nilai suku-suku yang berdekatan selalu sama.
Baca Juga:
Barisan dan Deret Aritmatika Beserta Contoh Soal
Contoh Soal suku ke-n Barisan Geometri
Diketahui barisan geometri 162,54,18,6,...
rumus suku ke-n barisan geometri tersebut adalah..
Pembahasan:
* Mencari nilai suku pertama dan rasio
a = U1 = 162
r = U3/U2 = 18/54 = 1/3
Un = ar(n-1)
Un = 162 × (1/3)(n-1)
Un = 162 × (1/3)(n) × 3
Un = 486 × (1/3)(n)
Misal kita uji coba denganmencari nilai Suku ke-4
U4 = 486 × (1/3)(4)
U4 = 486 × (1/81)
U4 = 6
B. Deret Geometri
Deret geometri adalah penjumlahan suku-suku dari suatu barisan geometri. Penjumlahan dari suku suku petama sampai suku ke-n barisan geometri dapat dihitung sebagai:
Sn = U1 + U2 + U3 + …. + U(n-1) + U(n)
Atau sebagai:
Sn = a + ar + ar2 + ar3 + …. + ar(n-2) + ar(n-1)
Rumus Jumlah n suku pertama Deret Geometri
Deret geometri merupakan jumlah dari suku-suku barisan geometri. Deret geometri bagi n suku pertama dinotasikan dengan penggunaan huruf Sn serta mempuyai rumus seperti berikut ini:
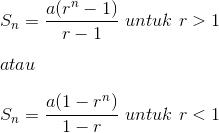
Contoh Soal Jumlah n suku pertama Deret Geometri
Diketahui deret geometri 3+9+27+....
a). Tentukan suku ke-6 dari deret tersebut
b). Tentukan S6 dari deret tersebut
Pembahasan:
a =3
r = U3/U2 = 9/3 = 3
a.) Mencari nilai suku ke-6
Un = ar(n-1)
U6 = 3 . 3 (6-1)
U6 = 3 . 3 (5)
U6 = 3 . 243
U6 = 729
b.) Mencari Jumlah 6 suku pertama, karena diketahui rasio lebih dari 1 maka gunakan rumus
Sn = a (rn - 1) / (r - 1)
S6 = 3 (36 - 1) / (3-1)
S6 = 3 (242) / 2
S6 = 3. 121
S6 = 363
Deret Geometri Tak Hingga Konvergen dan Divergen
Barisan geometri tak hingga masuk kategori konvergen jika suku ke tak hingga dari barisannya mendekati suatu nilai tertentu, dengan nilai rasio antara -1 dan 1.
Pada deret geometri, kekonvergenan bisa dilihat dari rasio deret tersebut.
Deret geometri tak hingga dikatakan konvergen jika dan hanya jika |r| < 1. Jumlah Deret geometri tak hingga konvergen dapat dihitung dengan rumus:
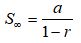
Sedangkan Deret geometri tak hingga dikatakan divergen dan tidak memiliki jumlah jika |r| ≥ 1.
Catatan :
-
|r| < 1 ≡ -1 < r < 1
-
|r| ≥ 1 ≡ r ≤ -1 atau r ≥ 1
Dari barisan dan deret tersebut, bisa dilihat antara suku pertama dengan suku kedua, antara suku kedua dan suku ketiga juga seterusnya selalu punya pengali (rasio) yang sama.
Contoh Soal Deret geometri tak hingga
Suku ke-2 dan suku ke-4 suatu deret geometri tak hingga berturut-turut adalah 1 dan 1/9. Jika rasionya positif, maka jumlah semua suku dari deret geometri itu adalah
Pembahasan:
U2 = 1 dan U4 = 1/9
Rasio deret ini dapat dihitung dengan melakukan perbandingan seperti berikut.
U4 / U2 = 1/9 /1
ar3 / ar = 1/9
r2 = 1/9
r2 = 1/32
r = 1/3
Karena rasionya diketahui positif, maka diambil r = 1/3
Selanjutnya, mari kita tentukan suku pertamanya.
U2 = ar
1 = a × 1/3
a = 3
Maka jumlah deret tersebut adalah
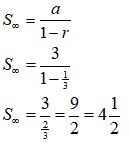
Demikian pembahasan materi Barisan dan Deret Geometri Beserta Soalnya yah otaker, semoga bermanfaat!
Artikel Terkait
- Hitunglah Deret Hingga Suku ke 8 Dari Barisan 1, 2, 4, 8, 16
- Diketahui jumlah deret geometri tak hingga adalah 15 dan suku pertamanya 6 rasio deret geometri tersebut adalah
- Dari hasil penelitian diperoleh data bahwa satu bakteri kolera berkembang biak dengan membelah diri setiap 30 menit untuk menghasilkan dua bakteri
- MENGHITUNG DERET GEOMETRI TAK HINGGA
- Cara Menghitung Jumlah Bakteri dengan Menggunakan Deret Geometri
- Soal Pembuktian Induksi Matematika dan Pembahasan || Part 2
- Soal Pembuktian Induksi Matematika dan Pembahasan || Part 1
- Deret Geometri Beserta Soal dan Pembahasan
- Prinsip Induksi Matematika, Contoh Soal dan Pembahasan
- Temukan Cara Cepat Mengerjakan Soal Barisan Aritmatika di Sini!