Bangun Ruang Kerucut Beserta Contoh Soal dan Pembahasan

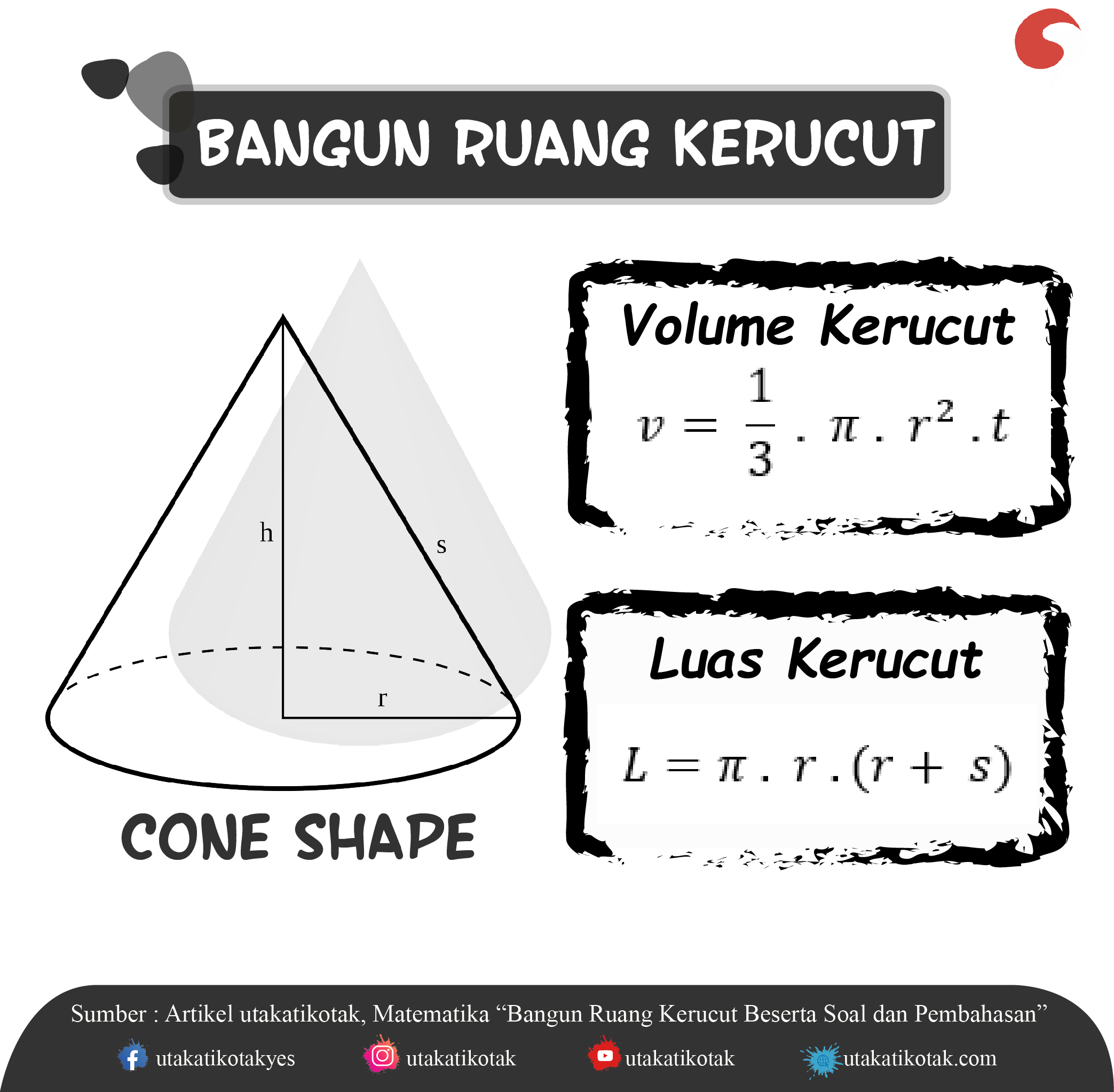
Otakers, artikel kali ini kita akan mengulas materi bangun ruang kerucut. Bangun ruang yang bentuknya seperti es cream cone atau topi caping petani milik petani. Nah, untuk kalian yang ingin lebih jauh mempelajari sifat-sifat bangun ruang kerucut dan rumus serta contoh soalnya, simak ulasan berikut ini yah !

Ciri-Ciri Bangun Ruang Kerucut

1. Kerucut adalah bangun ruang berbentuk limas yang alasnya berbentuk lingkaran

2. Kerucut memiliki 2 sisi,

3. Kerucut memiliki 1 rusuk,

4. Kerucut memiliki 1 titik puncak,

5. Kerucut memiliki Jaring-jaring kerucut yaitu lingkaran dan segitiga.

 Unsur-unsur Bangun Ruang Kerucut

1. Sisi alasnya berbentuk lingkaran berpusat pada titik A.

2. AC disebut tinggi dari kerucut.

3. Jari-jari lingkaran alas, yaitu AB dan diameternya BB’ = 2AB.

4. Sisi miring BC disebut apotema atau disebut juga garis pelukis.

5. Selimut kerucut berupa bidang lengkung.

Sifat- Sifat Bangun Ruang Kerucut

1. Kerucut memiliki 1 sisi alas berbentuk lingkaran dan 1 sisi berbentuk bidang lengkung (selimut kerucut).

2. Kerucut memiliki 1 rusuk lengkung.

3. Kerucut tidak memiliki titik sudut.

4. Kerucut memiliki 1 titik puncak

Rumus Bangun Ruang Kerucut

Volume Kerucut

V =  ¹/₃πr² t

Luas kerucut  = luas alas + luas selimut

• Luas alas kerucut = luas lingkaran = π x r x r = πr²

• Luas selimut kerucut = π x r x s

Luas kerucut  = luas alas + luas selimut

= (π x r x r) + (π x r x s)

= π x r ( r + s )

Luas = luas alas+luas selimut

atau

Luas = π x r ( r + s )

BACA JUGA : 

Rumus Volume Kerucut dan Contoh Soalnya!

Rumus Bangun Ruang: Kubus, Balok, Tabung, Bola dll

Soal Bangun Ruang Kerucut

1. Jika diameter kerucut I adalah 2 kali diameter kerucut II, tinggi kerucut I adalah sama dengan tinggi kerucut II. perbandingan volume kerucut I dan volume kerucut II adalah...

Jawab : perbandingan volume kerucut I dan volume kerucut II adalah 2 : 1

2. Sebuah kerucut tingginya 15 cm jika volume kerucut tersebut 6.930 cm kubik maka diameter kerucut kerucut tersebut

Jawab: 

V =  ¹/₃πr² t

6930 = 1/3 x 22/7 x r² x 15

6930 = 110/7 x r²

r² = 6930 x 7/110

r² = 441

r = 21

diameter = 2 x r = 2 x 21 = 42
Jadi diameter kerucut yaitu 42 cm

3. Sebuah kerucut memiliki jari jari 10cm dan tinggi 24cm tentukanlah:panjang garis pelukis kerucut,volume kerucut,luas selimut kerucut,dan luas seluruh kerucut

Jawab:

Dari soal diatas diketahui bahwa:

Jari-jari kerucut = r = 10 cm

Tinggi kerucut = t = 24

Maka,

Panjang garis pelukis kerucut = s = ?

s = √t² + r²

       = √24² + 10²

       = √576 + 100

       = √676

       = 26 cm

Volume kerucut = v =?

v = 1/3 x π x r² x t

  = 1/3 x 3,14 x 10 cm x 10 cm x 24 cm  

  = 2.512 cm³

Luas selimut kerucut = πrs

                                   = 3,14 x 10 x  26

                                   =  816,4 cm²          

Luas seluruh kerucut

  = π x r ( r + s )

  = 3,14 x 10 cm ( 10 cm + 26 cm )

  = 31,4 cm x 36 cm

  = 1130,4 cm²

4. Jika panjang jari jari kerucut A adalah 2 kali panjang jari jari kerucut B dan tinggi kerucut A sama dengan tinggi kerucut B, berapakah volume kerucut A dengan volume kerucut B??

Jawab:

dimana A=1 dan B=2

r₁=2r₂      

t₁=t₂

Volume Kerucut(1)=1/3 π r₁² t₁ .........(1)

Volume Kerucut (2) = 1/3 π r₂² t₂ .......(2)

substitusi r₁=2r₂ dan t₁=t₂ ke persamaan (1) diperoleh

Volume Kerucut (1) = 1/3 π (2r₂)²  t₂

                            = 1/3 π  4 r₂²  t₂

                            = 4 (1/3 π  r₂²  t₂)

                            = 4 Volume Kerucut (2)
Jadi Volume Kerucut A menjadi 4 kali Volume Kerucut B

5. Sebuah kerucut benda padat terdapat rongga ditengah yang berbentuk kerucut pula. Diameter kerucut 8 cm sedangkan diameter rongga kerucut sama dengan 1/2 diameter kerucut luar. Garis pelukis kerucut luar 10 cm. Tinggi kerucut rongga sama dengan 2/3 tinggi kerucut luar. Hitunglah
a. volume kerucut rongga
b. selisih antara kerucut luar dengan kerucut rongga

Jawab:

Ukuran kerucut luar:

r₁ = ½ diameter = ½ (8) = 4 cm

s₁ = 10 cm

t₁ = √(10² – 4²) = √(100 – 16) = √84 = 9,165 cm

Ukuran kerucut rongga:

d₂ = ½ diameter kerucut luar = ½ (8) = 4 cm

r₂ = ½ d₂ = ½ (4) = 2 cm

t₂ = 2/3 t₁= 2/3 (9,165) = 6,11 cm

a. Volume kerucut rongga = V₂

V₂ = 1/3 π r₂² t₂

      = 1/3 (3,14) (2)² (6,11)

      = 25,58 cm³

b. Yang ditanyakan selisih apa nih?

Jika yang ditanyakan selisih volume, hitung dulu volume kerucut luar (V₁), maka selisihnya adalah 

V₁ – V₂.

Simak ulasan materinya yah :