Apa Perbedaan Fungsi Injektif, Surjektif dan Bijektif ?

Otakers, sebelumnya kita sudah mempelajari Apa pengertian dari fungsi domain kodomain dan range bukan ?

Jika belum, pastikan kalian sudah membaca materi Pengertian Relasi, Fungsi, Domain, Kodomain dan Range agar tidak ketinggalan untuk membahas materi terkait sifat-sifat fungsi berikut ini.

Sifat-sifat Fungsi

Fungsi dikelompokkan menjadi 3 (tiga) jenis yaitu fungsi Injektif, Surjektif, dan Bijektif. Pengelompokkan tersebut didasarkan pada sifatnya.

Apa perbedaan fungsi injektif Surjektif dan bijektif?

Perbedaan ketiga jenis tersebut dapat disimak pada penjelasan di bawah.

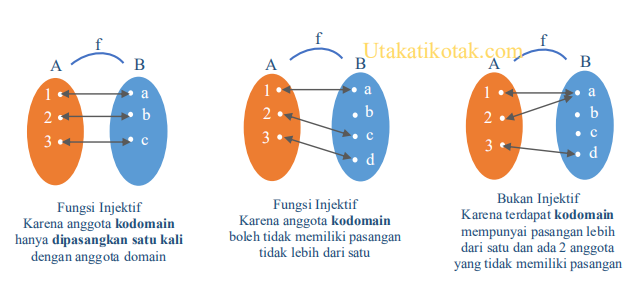
1. Fungsi Injektif/ Fungsi Satu-Satu (Fungsi Into)

Apa yang dimaksud dengan Injektif?

Fungsi injektif adalah fungsi into atau fungsi satu-satu.

Fungsi f: A → B dikatakan fungsi injektif 

-Jika dan hanya jika anggota kodomain hanya dipasangkan satu kali dengan anggota domain.

- Pada fungsi injektif, anggota himpunan daerah kodomain boleh tidak memiliki pasangan, namun semua anggota kodomain yang terpasangkan hanya ada satu, tidak boleh ada yang lebih dari satu.

Perhatikan gambar di bawah untuk melihat lebih detail mengenai perbedaannya.

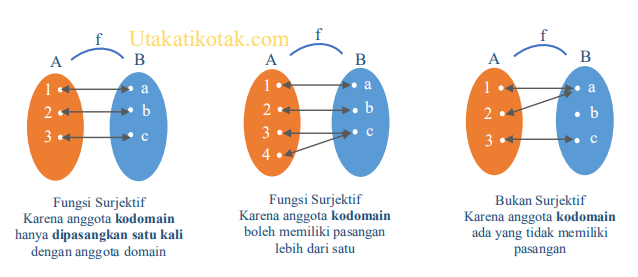
2. Fungsi Surjektif (Fungsi Onto)

Apa yang dimaksud dengan fungsi Surjektif ?

Fungsi Surjektif atau onto memiliki ciri-ciri yaitu anggota kodomainnya boleh memiliki pasangan lebih dari satu, namun tidak boleh ada anggota kodomain yang tidak dipasangkan. Fungsi surjektif biasanya dipenuhi apabila jumlah anggota kodomain sama atau lebih sedikit dari anggota domain.

Perhatikan gambar di bawah untuk menambah pemahaman sobat idschool tentang sifat fungsi surjektif.

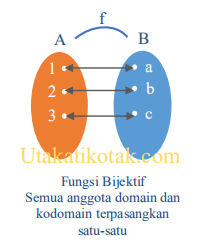
3. Fungsi Bijektif (Korespondensi Satu-Satu)

Apa yang dimaksud dengan Bijektif ?

Fungsi Bijektif adalah gabungan dari fungsi injektif dan surjektif. Pada fungsi bijektif, semua anggota domain dan kodomain terpasangkan tepat satu. Kebalikan fungsi dari fungsi injektif dan surjektif belum pasti fungsi/pemetaan, namun kebalikan fungsi dari fungsi bijektif juga merupakan fungsi/pemetaan.

Pemetaan bijektif terlihat seperti gambar di bawah.

Terlihat bahwa kebalikan dari fungsi f juga merupakan fungsi atau pemetaan, bukan?

Contoh Soal Injektif, Surjektif, dan Bijektif :

Sebutkan masing-masing sifat dari fungsi-fungsi berikut, dengan A = { -2, -1, 0, 1, 2} sebagai domain dan B = {0, 1, 2, 3, 4, 5} sebagai kodomain :
a. f(x) = 3 kurangnya dari
b. f(x) = akar kuadrat dari

Jawab

a. Range = {(-2,1), (-1, 2), (0,3), (1, 4), (2, 5)}

Jika dituliskan dalam diagram panah menjadi

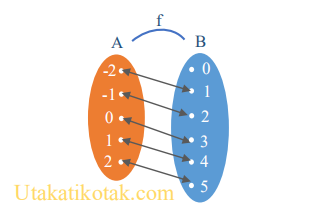
Merupakan Fungsi Injektif, karena terdapat satu anggota kodomain (B) yang tidak memiliki pasangan di daerah domain (A). Selain itu alasan lain adalah anggota kodomain hanya dipasangkan satu kali dengan anggota domain.

Tentu contoh diatas bukan termasuk Fungsi Surjektif, karena alasan yang sama, yaitu terdapat satu anggota kodomain (B) yang tidak memiliki pasangan di daerah domain (A)

b. Range = {(-2,4), (-1, 1), (0,0), (1, 1), (2, 4)}

Jika dituliskan dalam diagram panah menjadi

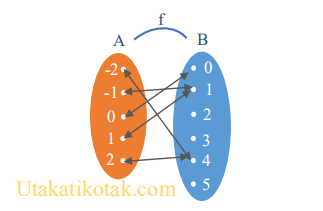
Nahh, jika dilihat pada gambar diagram panah diatas,

Bukan termasuk Fungsi Injektif karena anggota pada daerah kodomain (B) ada yang memiliki pasangan lebih dari satu di daerah domain (A).

Bukan termasuk fungsi Surjektif karena terdapat 3 anggota daerah kodomain (B) yang tidak memiliki pasangan di A.

Tentu juga Bukan Fungsi Bijektif karena tidak memasangkan tepat satu pada semua anggota. Berarti kesimpulannya dia termasuk Bukan Fungsi.

Baca Juga :

Pengertian Relasi, Fungsi, Domain,Kodomain dan Range

Fungsi Komposisi dan Fungsi Invers Lengkap dengan Soal

Bagaimana otakers, sudah paham belum nih perbedaan antara fungsi Injektif, surjektif, dan bijektif?

Semoga materi ini bisa membantu kalian dalam memahami perbedaan dari ketiga jenis fungsi diatas yah. Semangat !