Home » Kongkow » Matematika » Menggambar Grafik Fungsi Kuadrat

Menggambar Grafik Fungsi Kuadrat

- Jumat, 05 Maret 2021 | 11:00 WIB

Sebelum mempelajari langkah-langkah menggambar grafik fungsi kuadrat, perlu diketahui bahwa banyak materi dalam pelajaran Matematika yang saling berkaitan. Penguasaan materi dalam sebuah bab mempengaruhi pemahaman materi pada bab selanjutnya. Contohnya saja materi Fungsi Kuadrat. Cara menentukan faktor dari sebuah fungsi kuadrat, menggambar fungsi kuadrat berupa kurva mulus, dan mempelajari sifat-sifantya. Tidak sedikit murid merasa kesulitan ketika akan menggambar grafik fungsi kuadrat.

Sebanarnya ada cara yang dapat digunakan untuk menentukan gambaran umum dari grafik sebuah persamaan kuadrat dengan cara melihat nilai determinannya. Nilai Determinan dari sebuah fungsi kuadrat $f(x) = ax^{2} + bx + c$ adalah $D = b^{2} - 4ac$ . Determinan dapat digunakan untuk menyelidiki berapa banyak akar yang dimiliki sebuah persamaan kuadrat. Selain itu, determinan dapat digunakan untuk menentukan jenis akar yang dimiliki suatu persamaan kuadrat.

Karakteristik grafik berdasarkan nilai determinan:

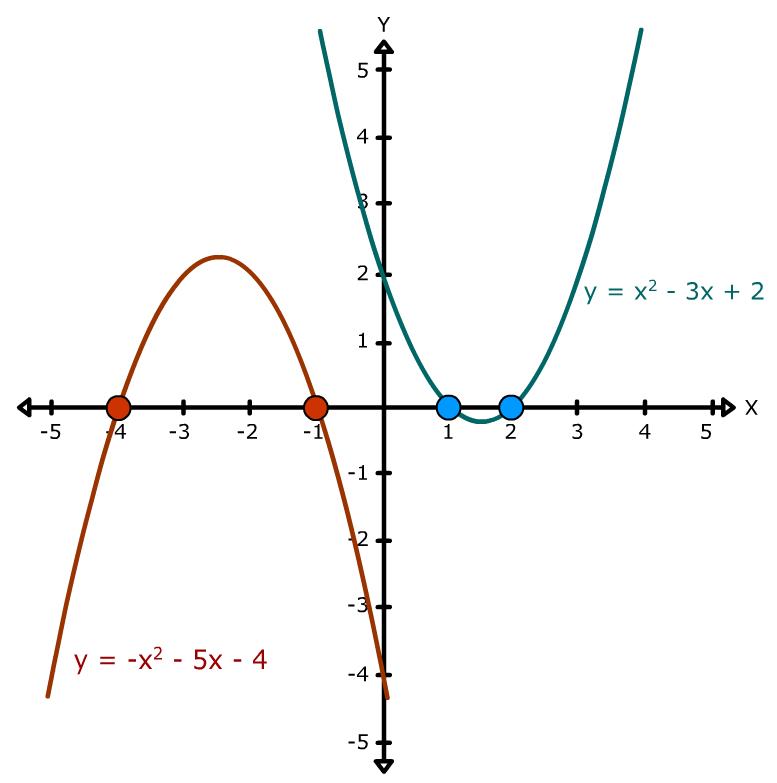
Jika D > 0 maka persamaan kuadrat memiliki dua akar real berbeda (artinya, grafik akan memotong sumbu x pada dua titik).
Jika D = 0 maka persamaan kudrat memiliki dua akar real kembar (artinya, grafik akan memotong sumbu x pada satu titik).
Jika D < 0 maka persamaan kuadrat memiliki akar yang imaginer/tidak real/akar negatif (artinya, grafik tidak memotong sumbu x).

Nilai (koefisien dari $x^{2}$ ) dapat memberi gambaran grafik fungsi kuadrat tersebut terbuka ke atas atau ke bawah. Karakteristik grafik berdasarkan nilai :

Jika a > 0 maka grafik akan terbuka ke atas.
Jika a < 0 maka grafik akan terbuka ke bawah.

Gambaran umum Grafik fungsi kuadrat jika dilihat dari nilai dan

Kriteria Grafik

Untuk menggambar grafik secara lebih detailnya dapat disimak dalam langkah-langkah berikut.

Langkah-langkah menggambar grafik fungsi kuadrat:

Tentukan titik potong dengan sumbu x (nilai y atau f(x) sama dengan 0).
Tentukan titik potong dengan sumbu y (nilai x = 0).
Menentukan sumbu simetri $x= -\frac{b}{2a}$ .
Menentukan titik puncak ( $-\frac{b}{2a}$ , $-\frac{b^{2} - 4ac}{4a}$ ) atau hitung nilai puncak y menggunakan substitusi/mengganti nilai x yang diperoleh pada perhitungan nomor 3 ke dalam persamaan f(x).

Empat langkah diatas sudah dapat digunakan untuk menggambar grafik persamaan kuadrat, jika perlu bisa menambahkan beberapa titik koordinat bantu.

Contoh Soal dan Pembahasan
Gambarlah grafik fungsi kuadrat $y = x^{2} - 2x - 8$ !

Secara sepintas kita akan mengetahui sketsa grafik menggunakan nilai a dan D:

Nilai artinya grafik akan terbuka ke atas.
Nilai $D = b^{2} - 4ac = (-2)^{2} - 4(1)(-8) = 4 + 32 = 36$ , nilai D > 0 artinya grafik akan memotong sumbu x pada dua titik.

Sketsa gambarnya kurang lebih akan seperti gambar di bawah.
Sketsa Grafik

Secara lebih detail, gambarnya dapat dilihat dengan mengikuti langkah-langkah berikut.
Langkah 1 Tentukan titik potong dengan sumbu x (nilai y atau f(x) sama dengan 0)

$y=0$

$x^{2} - 2x - 8 = 0$

$(x-4)(x+2) = 0$

$x = 4 \textrm{ atau } x = -2$

Jadi, diperoleh titik potong dengan sumbu x (4, 0) dan (-2, 0).

Langkah 1

Langkah 2 Tentukan titik potong dengan sumbu y (nilai x = 0)

$y = x^{2} - 2x - 8$

$y = 0^{2} - 0 - 8$

$y = - 8$

Jadi, titik potong dengan sumbu y adalah (0, -8).

Langkah 2

Langkah 3 Menentukan sumbu simetri $x = -\frac{b}{2a}$

$y = x^{2} - 2x - 8$

Diketahui: a = 1 , b = -2 , dan c = -8
maka sumbu simetri $x = -\frac{-2}{2} = 1$

Langkah 3

Langkah 4 Menentukan titik puncak ( $-\frac{b}{2a}$ , $-\frac{b^{2} - 4ac}{4a}$ )

$x = -\frac{b}{2a} = -\frac{-2}{2} = 1$

$y=-\frac{b^{2} - 4ac}{4a}=-\frac{(-2)^{2} - 4(1)(-8)}{4(1)} = -\frac{36}{4}=-9$

atau
substitusi nilai x = 1 (hasil perhitungan pada Langkah 3) pada persamaan $y = x^{2} - 2x - 8$ sehingga diperoleh

$y = 1^{2} - 2(1) - 8$

$= 1 - 2 - 8 = - 9$

Jadi, koordinat titk puncaknya adalah (1, – 9).

Langkah 4a

Selanjutnya tinggal menghubungkan titik-titik yang diperoleh sehingga menjadi kurva mulus seperti terlihat pada gambar berikut.

Grafik fungsi kuadrat

Demikianlah proses penggambaran grafik pada persamaan kuadrat, mudah bukan? Jika belum berhasil, jangan menyerah, pasti bisa! Coba lagi, coba lagi, dan coba lagi.
Semangat Belajar! Salam Prestasi!!!

Sumber :

Kuis Terkait

Video Terkait

Cari Artikel Lainnya

Menggambar Grafik Fungsi Kuadrat

Artikel Terkait

Kuis Terkait

Video Terkait