Menghitung Volume Benda Putar Menggunakan Integral

Salah satu aplikasi integral adalah menghitung volume benda putar. Benda putar pada dasarnya bisa diputar terhadap sumbu x dan sumbu y sehingga hasil dari perhitunga volumenya akan menjadi berbeda pula. Volume benda putar juga dapat diartikan sebagai ingral atau volume sebuah luasan yang diputar pada poros tertentu. Untuk memahami materi ini, ada beberapa materi yang harus dikuasai terlebih dahulu diantaranya sifat-sifat persamaan kuadrat, sifat-sifat akar kuadrat, penggambaran kurva, dan materi mengenai integral.

Rumus Volume benda putar Untuk Sumbu X dan Y

Metode yang dapat kita gunakan untuk menghitung volume benda putar menggunakan integral ada 2, yaitu :

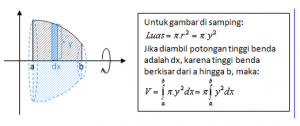
1. Metode Cakram

Berdasarkan rumus Volume = Luas Alas × tinggi
Luas Alas disini selalu berupa lingkaran maka Luas Alas = πr² (dimana r adalah jari-jari putaran)
digunakan jika batang potongan yang dipilih tegak lurus dengan sumbu putar

 

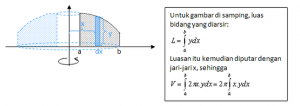
2. Metode Cincin Silinder

 

Menurut pengertian bahwa jika suatu luasan diputar terhadap sumbu tertentu, akan terbentuk suatu benda putar dengan volume sebesar luasan tersebut dikalikan dengan keliling putaran.
Dikarenakan  keliling lingkaran = 2πr, jika luas bidang yang diputar = A, maka volume = 2πr × A digunakan jika batang potongan sejajar dengan sumbu putar

Baca Juga :

Persamaan Garis Singgung Kurva

Cara Menghitung Luas Selimut Benda Putar

Agar dapat lebih memahami perhatikan beberapa contoh dibawah ini

1. Carilah volume benda putar yang terbentuk dari daerah yang dibatasi oleh kurva y = x², sumbu x, dan 0 ≤ x ≤ 2 jika diputar terhadap sumbu x?

Jawab :

 

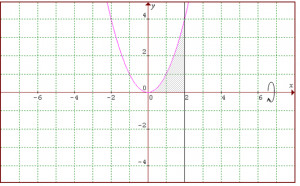
Menggunakan metode cakram

 

 

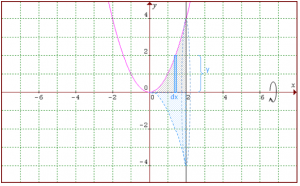
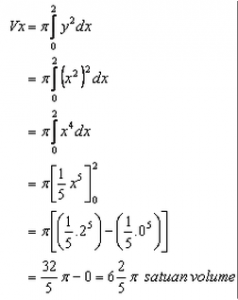
Menggunakan metode cincin silinder

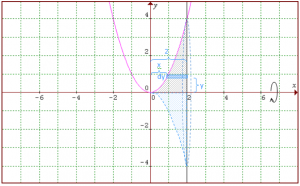
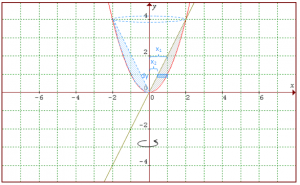
2. Carilah volume benda putar yang terjadi bila daerah yang dibatasi oleh kurva y = x² dan garis y = 2x diputar mengelilingi sumbu y?

Jawab :

Perpotongan kurva dan garis:

x² = 2x

x² – 2x = 0

x(x – 2) = 0

x = 0 atau x = 2

x = 0 → y = 0² = 0

x = 2 → y = 2² = 4

Jadi titik potong kurva dan garis adalah (0, 0) dan (2, 4)

Menggunakan Metode cakram:

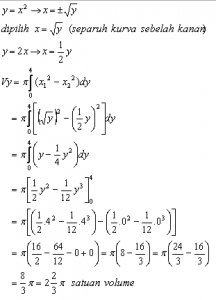
Menggunakan metode cincin silinder:

3. Jika daerah yang dibatasi oleh kurva x = (y – 2)² dan garis x + y = 4 diputar mengelilingi sumbu y, maka hitunglah volume benda putar yang terjad?

Jawab :

Perpotongan kurva dan garis:

x + y = 4 → x = 4 – y

(y – 2)² = 4 – y

y² – 4y + 4 = 4 – y

y² – 4y + 4 – 4 + y = 0

y² – 3y = 0

y(y – 3) = 0

y = 0 atau y = 3

y = 0 → x = 4 – 0 = 4

y = 3 → x = 4 – 3 = 1

Jadi titik potong kurva dan garis (4, 0) dan (1, 3)

Menggunakan metode cakram :

Menggunakan metode cincin silinder :

4. Hitunglah volume benda putar yang terjadi oleh daerah yang dibatasi  kurva y = x² dan y = 6x – x² jika diputar mengelilingi garis x = 4?

Jawab :

kurva hitam: y = x², kurva merah: y = 6x – x², garis biru: x = 4

Perpotongan kurva dan garis:

x² = 6x – x²

x² + x² – 6x = 0

2x² – 6x = 0

2x(x – 3) = 0

x = 0 atau x = 3

x = 0 → y = 0² = 0

x = 3 → y = 3² = 9

Menggunakan metode cakram :

Menggunakan metode cincin silinder :

5. Hitunglah volume benda putar yang terbentuk dari  daerah yang dibatai oleh kurva y = x² dan y = –x² + 4x jika diputar terhadap sumbu x?

Jawab :

Kurva merah: y = x², kurva hijau: y = –x² + 4x

Perpotongan kedua kurva:

x² = –x² + 4x

x² + x² – 4x = 0

2x² – 4x = 0

2x(x – 2) = 0

2x = 0 atau x = 2

x = 0 atau x = 2

x = 0 → y = 0² = 0

x = 2 → y = 2² = 4

Jadi perpotongan kedua kurva pada (0, 0) dan (2, 4)

Menggunakan metode cakram :

Menggunakan metode cincin silinder :

: