Rumus Volume Tabung dan Luas Permukaan Tabung Lengkap dengan Contoh Soal

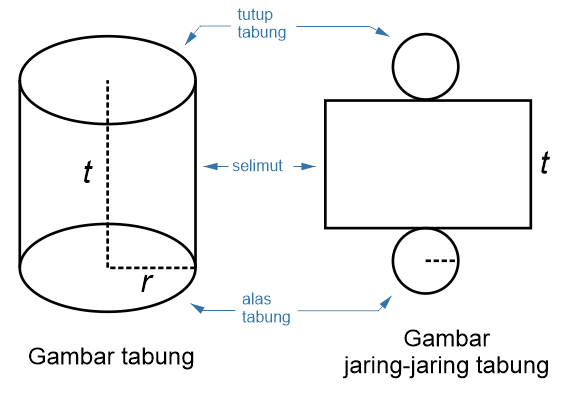
Tabung adalah bangun ruang yang tersusun oleh 3 buah sisi yaitu 2 buah lingkaran sebagai alas dan penutup yang mempunyai ukuran sama dan 1 segiempat yang menyelimuti kedua lingkaran tersebut.

Sifat-Sifat Tabung

Berikut sifat-sifat tabung:

• Tersusun dari 3 buah sisi, yaitu 2 lingkaran yang sama panjang dan 1 buah segiempat.

• 2 lingkaran pada tabung berperan sebagai tutup tabung dan alas tabung.

• Selimut tabung merupakan bangun segiempat yang mengelilingi tutup dan alas tabung.

• Tabung tidak mempunyai titik sudut.

• Tabung mempunyai 2 buah rusuk, yaitu rusuk yang mengelilingi alas dan tutup tabung.

• Jari-jari tabung adalah panjang jari-jari lingkaran yang membentuk tabung.

• Tinggi tabung adalah jarak yang memisahkan kedua lingkaran pada tabung.

 

Unsur – Unsur Tabung

• Sisi tabung
  Sisi tabung adalah bidang yang membentuk tabung. Sisi tabung terdiri dari dua buah lingkaran dan sebuah selimut.

• Selimut Tabung
  Selimut tabung adalah bidang yang menutupi bentuk tabung. Selimut tabung memiliki bentuk persegi panjang.

• Diameter
  Apabila salah satu alas atau tutup yang berbentuk lingkaran dipotong di tengah-tengah menjadi ukuran yang sama maka jarak potongan tersebut adalah diameter tabung.

• Jari-jari
  Jari-jari adalah setengah dari diameter tabung.

 

Rumus volume tabung

Apabila sebuah tabung diisikan air maka jumlah air yang dibutuhkan untuk mengisi tabung tersebut sampai penuh dinyatakan sebagai volume tabung.

Volume tabung adalah kapasitas ruang yang mampu ditampung oleh tabung. Rumus volume tabung yaitu :

V = Luas Alas x t

Keterangan :
V= volume tabung
t= tinggi tabung

 

Rumus luas permukaan tabung

Sebuah tabung terdiri dari tiga bidang penyusun yaitu dua buah lingkaran dan selimut. Bidang penyusun tabung memiliki luasan yang berbeda dimana luas dari bidang penyusunnya adalah

Alas atau tutup = π x r²

Selimut = K x t

Luas permukaan dari tabung adalah dua kali luas lingkarannya ditambah luas selimut atau:

Luas permukaan = (2 x Luas Alas) + Luas Selimut

Keterangan :
K= keliling alas atau tutup
π= phi (22/7 atau 3,14)
r= jari-jari
t= tinggi tabung

 

Contoh Soal

1. Diameter sebuah tabung 20 dm. Jika volume tabung 4.710 dm3. Berapa tinggo tabung tersebut

Pembahasan:

Volume tabung = phi x r² x t
4710                 = 3,14 x 10 x 10 x t
4710                 =  314 x t
15                     = t

jadi , tinggi tabung tersebut adalah 15 dm

 

2. Luas permukaan tabung adalah 1884 cm². jika tinggi tabung 20 cm.maka volume tabung adalah

Pembahasan:

Luas  = 2π.r.t
1.884 = 2 × 3,14 × 20 r
1.884 = 125,6 r
r         = 1.884/125,6
r         = 15 cm

V = π.r².t
V = 3,14 × 15² × 20
V = 62,5 × 225
V = 14.130 cm³

 

3. Sebuah Tabung memiliki t = 25cm dan r = 20cm, berapa volume tabung tersebut

Pembahasan:

Volume = Phi x r2 x t
             = 3,14 x 20 x 20 x 25
             = 31.400 cm3

 

4. Volume suatu tabung 120cm² jika tingginya di jadikan setengahnya maka volume tabung sekarang adalah

Pembahasan:

t2 = 1/2 x t1
r2 = r1
Volume sekarang = volume awal x (r2)² x t2
                            = 120 x 1² x 1/2
                            = 60 cm³

 

5. Jika volume tabung kecil 1/10volume tabung besar. Berapa volume kedua tabung tersebut (p=22/7)

Pembahasan:

Tabung besar,
volume = 1/4 x pi x d x d x t
volume = 1/4 x 22/7 x 14 x 14 x 20
volume = 3.080 cm kubik

Tabung kecil
volume = volume 1/10 tabung besar
volume = 1/10 x 3.080
volume = 308 cm kubik

total volume = 3.080 + 308
total volume = 3.388 cm kubik