Materi Lengkap Cermin dan Lensa

Materi Cermin Cekung
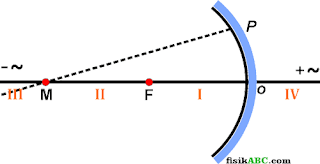
Cermin cekung (konkaf) adalah cermin lengkung yang bagian dalamnya dapat memantulkan cahaya. Cermin cekung disebut juga cermin positif atau cermin konvergen, karena sifat cermin cekung yang mengumpulkan atau memusatkan sinar yang jatuh padanya. Bagian-bagian cermin cekung, diperlihatkan pada gambar berikut ini.
Sifat-Sifat Bayangan Cermin Cekung
Bayangan yang dibentuk oleh cermin cekung bisa berupa bayangan nyata atau maya. Hal ini bergantung pada tempat benda semula berada. Berikut ini adalah daftar posisi benda, sifat bayangan dan letak bayangan pada peristiwa pemantulam cahaya pada cermin cekung.
| Posisi Benda | Sifat Bayangan | Letak Bayangan |
| Ruang I | Maya, tegak, diperbesar | Di belakang cermin |
| Titik Fokus | Maya, tegak, diperbesar | Di belakang cermin |
| Ruang II | Nyata, terbalik, diperbesar | Di depan cermin |
| Pusat Kelengkungan | Nyata, terbalik, sama besar | Di depan cermin |
| Ruang III | Nyata, terbalik, diperkecil | Di depan cermin |
Rumus-Rumus Pada Cermin Cekung
Pada cermin cekung, hubungan antara jarak benda (s) dan jarak bayangan (s’) akan menghasilkan jarak fokus (f). Hubungan tersebut secara matematis dapat ditulis sebagai berikut.
| 1 | = | 1 | + | 1 |
| f | s | s' | ||
| 2 | = | 1 | + | 1 |
| R | s | s' |
Keterangan:
s = jarak benda
s’ = jarak bayangan
f = jarak fokus
R = jari-jari cermin
Sementara perbesaran bayangan (M) dapat dicari melalui perbandingan antara tinggi bayangan dengan tinggi benda atau jarak bayangan dengan jarak benda yang dirumuskan sebagai berikut.
| M | = | h' | = | s’ |
| h | s |
Keterangan:
M = perbesaran bayangan
h' = tinggi bayangan
h = tinggi benda
s’ = jarak bayangan
s = jarak benda
Sedangkan rumus untuk menentukan nomor ruang benda dan nomor ruang bayangan pada cermin cekung, secara matematis dituliskan dalam bentuk persamaan berikut ini.
| Nomor ruang benda + nomor ruang bayangan = V |
Contoh Soal Cermin Cekung dan Pembahasan
Benda setinggi 6 cm berada di depan cermin cekung yang berjari-jari 30 cm. bila jarak benda ke cermin 20 cm, maka tentukanlah jarak bayangan, perbesaran bayangan, tinggi bayangan dan sifat bayangan.
Penyelesaian:
Diketahui:
h = 6 cm
R = 30 cm
s = 20 cm
f = ½ R = 15 cm
Ditanyakan: s’, M, h dan sifat bayangan.
Jawab
■ Jarak bayangan
1/f = 1/s + 1/s’
1/15 = 1/20 + 1/s’
1/s’ = 1/15 – 1/20
1/s’ = 4/60 – 3/60
1/s’ = 1/60
s' = 60 cm
Jadi, bayangan benda berada di depan cermin dengan jarak 60 cm.
■ Perbesaran bayangan
M = |s’/s|
M = |60/20|
M = 3x
Jadi, perbesaran bayangan benda adalah 3x dari benda aslinya.
■ Tinggi Bayangan
M = h’/h
3 = h’/6
h' = 3 × 6
h' = 18 cm
Jadi, tinggi bayangan benda adalah 18 cm.
■ Sifat Bayangan
Dari perhitungan di atas kita peroleh data berikut.
s' = 60 cm
h' = 18 cm
• s’ bernilai positif maka bayangan berada di depan cermin sehingga bersifat nyata dan terbalik.
• h’ > h sehingga bayangan bersifat diperbesar.
Dengan demikian, sifat bayangan yang terbentuk adalah nyata, terbalik dan diperbesar.
b. Materi Cermin Cembung
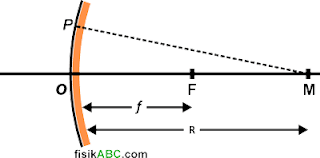
Cermin cembung (konveks) adalah cermin lengkung yang bagian luarnya dapat memantulkan cahaya. Cermin cembung disebut juga cermin negatif dan cermin divergen, karena cermin cekung menyebarkan sinar cahaya yang jatuh pada permukaannya. Adapun bagian-bagian cermin cekung, diperlihatkan pada gambar berikut ini.
Sifat-Sifat Bayangan Cermin Cembung
Adapun sifat-sifat bayangan yang dibentuk oleh cermin cembung adalah sebagai berikut.
| □ | Maya |
| □ | Tegak |
| □ | Diperkecil |
| □ | Terletak di belakang cermin, yaitu di antara titik pusat optik (O) dan titik fokus (F) |
| □ | Jarak bayangan lebih kecil dari jarak benda (s’ < s) |
| □ | Jarak bayangan selalu bernilai negatif (s’ = −) |
Rumus-Rumus Pada Cermin Cembung
Rumus-rumus pada cermin cekung juga berlaku pada cermin cembung. Hanya saja jarak fokus (f) dan jari-jari kelengkungan cermin (R) pada cermin cembung berharga negatif. Rumus-rumusnya yaitu sebagai berikut.
| 1 | = | 1 | + | 1 |
| −f | s | s' | ||
| 2 | = | 1 | + | 1 |
| −R | s | s' |
Keterangan:
s = jarak benda
s’ = jarak bayangan
f = jarak fokus
R = jari-jari cermin
Beberapa hal yang perlu diperhatikan adalah:
| □ | Tanda jarak fokus pada cermin cembung selalu bernilai negatif. Hal ini disebabkan letak titik fokus pada cermin cembung terletak di belakang cermin. |
| □ | Untuk benda nyata di depan cermin cembung, selalu terbentuk bayangan maya. Jadi, nilai s’ pada cermin cembung selalu bertanda negatif |
Sementara perbesaran bayangan (M) dapat dicari melalui perbandingan antara tinggi bayangan dengan tinggi benda atau jarak bayangan dengan jarak benda yang dirumuskan sebagai berikut.
| M | = | h' | = | s’ |
| h | s |
Keterangan:
M = perbesaran bayangan
h' = tinggi bayangan
h = tinggi benda
s’ = jarak bayangan
s = jarak benda
Contoh Soal Cermin Cembung dan Pembahasan
Benda setinggi 10 cm, berada di depan cermin cembung yang memiliki jari-jari 80 cm. Bila jarak benda 60 cm, maka tentukan letak bayangan, perbesaran bayangan dan tinggi bayangan!
Penyelesaian:
Diketahui:
h = 10 cm
s = 60 cm
R = 80 cm = −80 cm (dibelakang cermin)
f = ½R = ½(−80 cm) = −40 cm
Ditanyakan: s’, M dan h
Jawab:
■ Jarak bayangan
1/−f = 1/s + 1/s’
1/−40 = 1/60 + 1/s’
1/s’ = 1/−40 − 1/60
1/s’ = −3/120 − 2/120
1/s’ = −5/120
s' = 120/−5
s' = −24 cm
Jadi, bayangan benda berada di belakang cermin pada jarak 24 cm.
■ Perbesaran bayangan
M = |s’/s|
M = |−24/60|
M = 0,4x
Jadi, bayangan benda mengalami perbesaran 0,4x (bayangan benda lebih kecil).
■ Tinggi Bayangan
M = h’/h
0,4 = h’/10
h' = 0,4 × 10
h' = 4 cm
Jadi, tinggi bayangan benda adalah 4 cm.
LENSA
a. Lensa Cekung
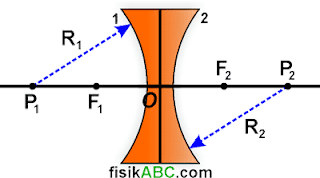
Lensa cekung merupakan lensa yang permukaan lengkungnya menghadap ke dalam. Ciri utama lensa cekung adalah bagian tengah lebih tipis daripada bagian pinggir atau tepi. Berbeda dengan lensa cembung yang mengumpulkan sinar (konvergen), lensa cekung memiliki sifat memancarkan/menyebarkan sinar (divergen). Adapun bagian-bagian lensa cekung diilustrasikan pada gambar berikut.
Sifat-Sifat Bayangan Lensa Cekung
Adapun sifat-sifat bayangan yang dibentuk oleh lensa cekung adalah sebagai berikut.
| □ | Maya |
| □ | Tegak |
| □ | Diperkecil |
| □ | Terletak di depan lensa, yaitu di antara titik pusat optik (O) dan titik fokus aktif (F1). |
| □ | Jarak bayangan lebih kecil dari jarak benda (s’ < s) |
| □ | Jarak bayangan selalu bernilai negatif (s’ = −) |
Rumus-Rumus Pada Lensa Cekung
Pada lensa cekung, hubungan antara jarak benda (s) dan jarak bayangan (s’) akan menghasilkan jarak fokus (f). Hubungan tersebut secara matematis dapat ditulis sebagai berikut.
| 1 | = | 1 | + | 1 |
| f | s | s' | ||
| 2 | = | 1 | + | 1 |
| R | s | s' |
Keterangan:
s = jarak benda
s’ = jarak bayangan
f = jarak fokus
R = jari-jari lensa
Beberapa hal yang perlu diperhatikan adalah:
| □ | Tanda jarak fokus pada lensa cekung selalu bernilai negatif. Hal ini disebabkan letak titik fokus aktif (utama) pada lensa cekung terletak di depan lensa. |
| □ | Untuk benda nyata di depan lensa cekung, selalu terbentuk bayangan maya. Jadi, nilai s’ pada lensa cekung selalu bertanda negatif. |
Sementara perbesaran bayangan (M) dapat dicari melalui perbandingan antara tinggi bayangan dengan tinggi benda atau jarak bayangan dengan jarak benda yang dirumuskan sebagai berikut.
| M | = | h' | = | s’ |
| h | s |
Keterangan:
M = perbesaran bayangan
h' = tinggi bayangan
h = tinggi benda
s’ = jarak bayangan
s = jarak benda
Lensa cekung memiliki kemampuan untuk menyebarkan sinar cahaya. Kemampuan ini disebut kekuatan lensa. Semakin kecil jarak fokus lensa, semakin besar kekuatan lensa untuk menyebarkan sinar. Kekuatan lensa cekung dirumuskan sebagai berikut.
| P | = | 1 |
| f |
Keterangan:
P = kekuatan lensa (dioptri = D)
f = jarak fokus (m)
Contoh Soal Lensa Cekung dan Pembahasan
1. Sebuah benda setinggi 1 cm berada di depan lensa cekung dengan fokus 2 cm. Jika jarak benda 4 cm maka tentukanlah jarak bayangan, perbesaran bayangan, tinggi bayangan dan sifat bayangan.
Penyelesaian:
Diketahui:
h = 1 cm
s = 4 cm
f = −2 cm
Ditanyakan: s’, M, h’, dan sifat bayangan.
Jawab:
■ Jarak bayangan dihitung dengan menggunakan rumus berikut:
1/f = 1/s + 1/s’
1/−2 = 1/4 + 1/s’
1/s’ = 1/−2 − 1/4
1/s’ = −2/4 − 1/4
1/s’ = −3/4
s' = 4/−3
s' = −1,3 cm
Jadi, jarak bayangan adalah 1,3 cm di depan lensa.
■ Perbesaran bayangan dapat ditentukan dengan menggunakan rumus berikut:
M = |s’/s|
M = |−1,3/4|
M = 0,3 = 1/3
Jadi, bayangan benda mengalami perbesaran 1/3x (bayangan benda lebih kecil).
■ Tinggi bayangan dapat dicari dengan menggunakan rumus perbesaran bayangan, yaitu sebagai berikut.
M = h’/h
1/3 = h’/1
h' = 1/3 × 1
h' = 0,3 cm
Jadi, tinggi bayangan benda adalah 0,3 cm.
■ Dari hasil perhitungan s’ dan M maka sifat bayangan ditentukan dengan cara berikut:
1. Karena s’ bernilai negatif (−) maka bayangan bersifat maya dan tegak
2. Karena M = 1/3 < 1, maka bayangan diperkecil.
Jadi, sifat bayangan yang terbentuk oleh lensa cekung adalah maya tegak dan diperkecil. Sebenarnya, sifat bayangan yang dibentuk oleh lensa cekung selalu sama jadi kita tidak perlu menggunakan perhitungan ataupun melukis pembentukan bayangan dalam menentukan sifat bayangan pada lensa cekung.
2. Jika sebuah lensa bikonkaf memiliki kekuatan lensa 1,5 dioptri, berapakah jarak fokus lensa tersebut?
Penyelesaian:
Diketahui:
Lensa = bikonkaf (cekung)
P = −1,5 dioptri
Ditanyakan: f
Jawab:
P =1/f
f = 1/P
f = 1/−1,5
f = −0,67
Jadi, lensa tersebut memiliki jarak titik fokus lensa 0,67 m = 67 cm.
a. Lensa Cembung
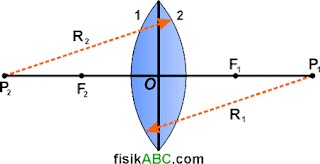
Lensa cembung adalah lensa dengan bagian tengah lebih tebal daripada bagian tepi. Cahaya yang jatuh pada permukaan lensa cembung akan mengalami pembiasan. Berkas-berkas sinar datang akan dibiaskan sehingga berkas-berkas sinar biasnya mengumpul. Oleh karena itu, lensa cembung disebut juga lensa konvergen. Adapun bagian-bagian lensa cembung ditunjukkan pada gambar berikut ini.
Sifat-Sifat Bayangan Lensa Cembung
Letak dan sifat bayangan yang dibentuk oleh lensa cembung bergantung pada letak benda. Sebuah objek yang diletakkan di depan sebuah lensa cembung akan memiliki bayangan dengan sifat tertentu. Berikut ini adalah daftar posisi benda, sifat bayangan dan letak bayangan pada peristiwa pembiasan cahaya pada lensa cembung.
| Posisi Benda | Sifat Bayangan | Letak Bayangan |
| Ruang I | Maya, tegak, diperbesar | Di depan lensa |
| Titik Fokus | Maya, tegak, diperbesar | Di depan lensa |
| Ruang II | Nyata, terbalik, diperbesar | Di belakang lensa |
| Pusat Kelengkungan | Nyata, terbalik, sama besar | Di belakang lensa |
| Ruang III | Nyata, terbalik, diperkecil | Di belakang lensa |
Berdasarkan tabel di atas, maka dapat kita simpulkan beberapa hal mengenai sifat bayangan yang dibentuk oleh lensa cembung, yaitu sebagai berikut.
| □ | Semua bayangan maya yang dibentuk lensa cembung selalu tegak terhadap bendanya. |
| □ | Semua bayangan nyata yang dibentuk lensa cembung pasti terbalik terhadap bendanya. |
Rumus-Rumus Pada Lensa Cembung
Pada lensa cembung, hubungan antara jarak benda (s) dan jarak bayangan (s’) akan menghasilkan jarak fokus (f). Hubungan tersebut secara matematis dapat ditulis sebagai berikut.
| 1 | = | 1 | + | 1 |
| f | s | s' | ||
| 2 | = | 1 | + | 1 |
| R | s | s' |
Keterangan:
s = jarak benda
s’ = jarak bayangan
f = jarak fokus
R = jari-jari lensa
Sementara perbesaran bayangan (M) dapat dicari melalui perbandingan antara tinggi bayangan dengan tinggi benda atau jarak bayangan dengan jarak benda yang dirumuskan sebagai berikut.
| M | = | h' | = | s’ |
| h | s |
Keterangan:
M = perbesaran bayangan
h' = tinggi bayangan
h = tinggi benda
s’ = jarak bayangan
s = jarak benda
Pada lensa cembung, makin kecil jarak titik fokusnya, maka makin kuat lensa tersebut memancarkan sinar. Hal ini berarti bahwa kekuatan lensa berbanding terbalik dengan jarak titik fokusnya. Secara matematis, kekuatan lensa dirumuskan sebagai berikut.
| P | = | 1 |
| f |
Keterangan:
P = kekuatan lensa (dioptri = D)
f = jarak fokus (m)
Sedangkan rumus untuk menentukan nomor ruang benda dan nomor ruang bayangan pada lensa cembung, secara matematis dituliskan dalam bentuk persamaan berikut ini.
| Nomor ruang benda + nomor ruang bayangan = V |
Contoh Soal Lensa Cembung dan Pembahasan
1. Untuk menentukan tinggi bayangan, elemen-elemen yang harus kita ketahui terlebih dahulu adalah jarak bayangan (s’) dan perbesaran bayangan (M).
■ Jarak bayangan
1/f = 1/s + 1/s’
1/s’ = 1/f – 1/s
1/s’ = 1/8 – 1/12
1/s’ = 3/24 – 2/24
1/s’ = 1/24
s’ = 24/1
s’ = 24 cm
■ Perbesaran bayangan
M = |s’/s|
M = |24/12|
M = 2
Dari dua perhitungan di atas, kita peroleh s’ = 24 cm dan M = 2. Sehingga, tinggi bayangan dapat kita tentukan dengan cara berikut.
M = |h’/h|
2 = h’/3
h' = 2 × 3 = 6
Dengan demikian, tinggi bayangannya adalah 6 cm.
2. Berapakah kekuatan lensa sebuah lensa bikonveks dengan jarak titik fokus 10 cm?
Penyelesaian:
Lensa = bikonveks (berarti lensa cembung, sehingga f dan P bernilai positif)
f = 10 cm = 0,1 m
Ditanyakan: P
Jawab:
P = 1/f
P = 1/0,1 = 10
Jadi, lensa tersebut memiliki kekuatan 10 dioptri.
Artikel Terkait
- asd
- asd
- Sinonim akulturasi adalah kontak kabudayaan #sinonim #bahasa #akulturaasi #bahasaindonesia #antonim
- Pada Suatu Pertemuan, Hadir 10 Orang yang Saling Berjabat Tangan. Banyaknya Jabat Tangan yang Terjadi Adalah... Jawaban dan Pembahasan
- Suku Kelima Suatu Barisan Aritmatika Adalah 22, Sedangkan Kesembilan Adalah 42. Suku Kelima Belas Sama Dengan... Jawaban dan Pembahasan
- Mata Uang yang Sering Digunakan Sebagai Alat Pembayaran dan Kesatuan Hitung Dalam Transaksi Ekonomi dan Keuangan Internasional Disebut...
- Kingdom yang Tidak Memiliki Dinding Sel... Jawaban dan Pembahasan
- Organel Sel yang Berperan Untuk Mendetoksifikasi Racun Adalah... Jawaban dan Pembahasan
- Diketahui Harga 4 kg Jeruk, 1 kg Semangka, dan 2 kg Apel Adalah Rp 54.000,00. Harga 1 kg Jeruk, 2 kg Semangka, dan 2 kg Apel Adalah Rp 43.000,00. Sedangkan Harga 3 kg Jeruk, 1 kg Semangka, dan 1 kg Apel Adalah Rp 37.500,00. Berapakah Harga 1 kg Semangka?
- Nilai Rataan Hitung dari Data 4 10 7 x 10 6 11 Adalah 8 Nilai x Adalah ...