Prinsip Kerja Hukum Bernoulli Beserta Penerapannya

Fluida ideal yang memenuhi Hukum Bernoulli adalah fluida ideal yang memenuhi karakteristik mengalir dengan garis-garis arus atau aliran tunak, tak komprisebel dan tak kental. (Nurohman:10)

Prinsip Bernoulli merupakan turunan dari hukum-hukum dasar mekanika Newton, yaitu akan diturunkan dari teorema kerja-tenaga karena Persamaan Bernoulli pada pokoknya adalah sebuah pernyataan teorema  kerja-tenaga untuk aliran flluida. Teorema kerja-tenaga menyatakan Kerja yang dilakukan oleh gaya resultan yang beraksi pada sebuah sistem adalah sama dengan perubahan tenaga kinetik dari sisten tersebut. (Resnick, 1985: 584-585)

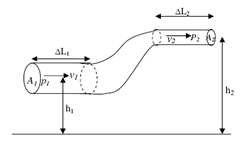
 Persamaan Bernoulli menyatakan bahwa:

P₁ + ½ ρv₁² + ρgh₁ = P₂ + ½ ρv₂² + ρgh₂

Karena indeks bawah 1 dan 2 menunjukan dua tempat yang sembarang sepanjang pipa tersebut, maka dapat dihapuskan indeks bawah tersebut, sehingga persamaan dapat disajikan :

P + ½ ρv² + ρgh = konstan

Keterangan :

P   = tekanan (Pa)

ρ  = massa jenis zat cair/fluida (kg/ m³)

v   = kecepatan aliran fluida (m/s)

g   = percepatan gravitasi (m/s²).

h   = ketinggian (m).

 

Persamaan Bernoulli dapat digunakan untuk menentukan laju fluida dengan cara mengukur tekanan. Prinsip yang umum digunakan di dalam alat pengukur seperti itu adalah sebagai berikut: persamaan kontinuitas mengharuskan bahwa laju fluida ditempat penyempitan akan bertambah besar. Persamaan Bernoulli kemudian memperlihatkan bahwa tekanan haris turun di tempat tersebut.

Penerapan Hukum Bernoulli dalam kehidupan sehari-hari diuraikan sebagai berikut:

 

1. Teori Torricelli

Persamaan Bernoulli  dapat  digunakan untuk menentukan kecepatan zat cair yang keluar dari lubang pada dinding tabung. Dengan menganggap diameter tabung lebih besar dibandingkan  diameter lubang, maka permukaan zat cair pada tabung turun perlahan-lahan, sehingga kecepatan v₁ dapat  dianggap nol seperti ditunjukkan gambar di bawah ini:

 

 

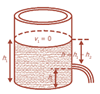
Titik 1 (permukaan) dan titik 2 (lubang) terbuka terhadap udara sehingga tekanan pada kedua titik sama dengan tekanan atmosfer, P₁ = P₂ sehingga persamaan Bernoulli dinyatakan (Haryadi, 2009:162):

½ ρv₂² + ρgh₂ = 0 + ρgh₁

½ ρv₂² = ρg(h₁ – h₂)

v = √2g (h₁ – h₂) = √2gh

Persamaan di atas disebut teori Torricelli, yang menyatakan bahwa kecepatan aliran zat cair pada lubang sama dengan kecepatan benda yang jatuh bebas dari ketinggian yang sama.

 

2. Venturimeter

Venturimeter adalah alat yang digunakan untuk mengukur laju aliran zat cair dalam pipa.  Zat cair dengan  massa jenis ρ  mengalir melalui pipa yang luas penampangnya A₁. Sedangkan, pada pipa yang sempit dengan luas penampang A₂.

 
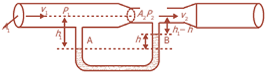
Berdasarkan gambar di atas dari persamaan kontinuitas pada titik 1 dan 2 dapat dinyatakan:

A₁v₁ = A₂v₂

v₂ = (A₁v₁)/A₂

Berdasarkan persamaan Bernoulli, berlaku (Haryadi, 2009:163):

P₁ + ½ ρv₁² + ρgh₁ = P₂ + ½ ρv₂² + ρgh₂

Karena h₁ = h₂, maka:

P₁ + ½ ρv₁² = P₂ + ½ ρv₂²

Baca Juga :

Tegangan Permukaan Zat Cair

Rumus dan Pembahasan Fluida Statis Lengkap

Perbedaan Fluida Statis dan Dinamis

Jika persamaan v₂ disubtitusikan maka akan dihasilkan:

P₁ + ½ ρv₁² = P₂ + ½ ρ(A₁/A₂)² v₁²

P₁ – P₂ = P₂ + ½ ρv₁²[(A₁² – A₂²)/A₂²

Berdasarkan persamaan tekanan hidrostatik, pada manometer berlaku:

P_A = P₁ + ρgh₁

P_B = P₂ + ρg(h₁ – h) + ρ’gh

Titik A dan B berada pada satu bidang mendatar, maka berlaku Hukum Pokok Hidrostatika.

P_A = P_B

P₁ + ρgh₁ = P₂ + ρg(h₁ – h) + ρ’gh

P₁ = P₂ – ρgh + ρ’gh

P₁ – P₂ = ρ’gh – ρgh

P₁ – P₂ = (ρ’ – ρ) gh

Dari persamaan di atas, diperoleh:

½ ρv₁²[(A₁² – A₂²)/A₂² = (ρ’ – ρ) gh

Sehingga:

v₁ = A₂ √[2(ρ’ – ρ) gh]/ 2[(A₁² – A₂²)/A₂²]

Keterangan :

v₁ = laju aliran fluida pada pipa besar (m/s)

A₁ = luas penampang pipa besar (m²)

A₂ = luas penampang pipa kecil (m²)

ρ =  massa jenis fluida (kg/m³)

ρ’ = massa jenis fluida dalam manometer (kg/m³)

h =  selisih tinggi permukaan fluida pada manometer (m)

g =   percepatan gravitasi (m/s²)

Untuk venturimeter tanpa dilengkapi manometer pada prinsipnya sama, tabung manometer diganti dengan pipa pengukur beda tekanan seperti gambar di bawah ini (Haryadi, 2009:163).

Sehingga didapatkan persamaan:

 

P₁ – P₂ = ½ ρ(v₂² – v₁²)

dengan memasukkan v₂ = (A₁v₁)/A₂ maka diperoleh persamaan sebagai berikut:

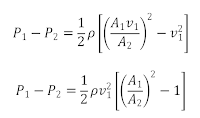
 Berdasarkan persamaan tekanan hidrostatik, maka tekanan pada titik 1 dan 2 adalah:

 

P₁ = P_o + ρgh

P₂ = P_o + ρgh

Selisih tekanan pada kedua penampang adalah:

P₁ – P₂ = ρg (h₁ – h₂) = ρgh

Dengan menggabungkan kedua persamaan yang melibatkan perbedaan tekanan tersebut diperoleh kelajuan aliran fluida:

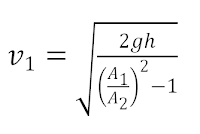
Keterangan:

v₁ = laju aliran fluida pada pipa besar (m/s)

A₁ = luas penampang pipa besar (m²)

A₂ = luas penampang pipa kecil (m²)

h   = selisih tinggi permukaan fluida pada manometer (m)

g   = percepatan gravitasi (m/s²)

 

3. Gaya Angkat Pesawat Terbang

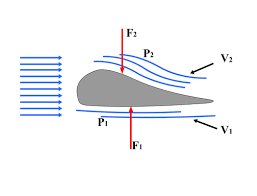
Pesawat terbang dapat terangkat ke udara karena kelajuan udara yang melalui sayap pesawat.  Penampang sayap pesawat terbang mempunyai bagian belakang yang lebih tajam dan sisi bagian atas yang lebih melengkung daripada sisi bagian bawahnya.

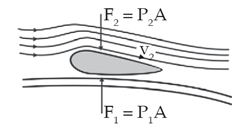
Daya angkat dinamik adalah gaya yang beraksi pada sebuah benda, seperti sayap  kapal terbang, rotor helikopter, hidrofil, karena geraknya melalui suatu fluida. Sudut serangan (angel of attack) sayap menyebabkan udara menyimpang ke bawah. Dari hukum Newton ketiga maka reaksi gaya sayap yang mengarah ke bawah ini pada udara adalah sebuah gaya F yang arahnya ke atas, yakni daya angkat tersebut yang dikerahkan oleh udara pada sayap.

 

Pola garis-garis ars adalah konsisten. Di atas sayap garis-garis arus adalah lebih dekat satu sama lain daripada di bawah sayap. Jadi v₁ > v₂ dan dari prinsip Bernoulli P₁ < P₂ yang harus benar supaya ada daya angkat. (Resnick, 1985: 590)