Home » Kongkow » Materi » Memahami Kesetimbangan Benda Tegar Melalui Pembahasan Soal

Memahami Kesetimbangan Benda Tegar Melalui Pembahasan Soal

- Rabu, 15 September 2021 | 11:00 WIB

Kesetimbangan benda tegar adalah kondisi dimana momentum benda tegar sama dengan nol. Artinya jika awalnya benda tegar tersebut diam, maka ia akan tetap diam. Namun jika awalnya benda tegar tersebut bergerak dengan kecepatan konstan, maka ia akan tetap bergerak dengan kecepatan konstan.

Sedangkan benda tegar sendiri adalah benda yang bentuknya (geometrinya) akan selalu tetap sekalipun dikenakan gaya. Jadi sekalipun dia bergerak translasi atau rotasi bentuknya tidak akan berubah, contohnya meja, kursi, bola, dll.

Perlu diperhatikan bahwa momentum terbagi menjadi dua, yakni momentum linear dan momentum angular. Pertama-tama kita meninjau momentum linear p = 0. Momentum linear dan impuls dihubungkan oleh persamaan

$\Sigma F \cdot \Delta t = \Delta p$ dapat juga ditulis menjadi $\Sigma F = \frac{\Delta p}{\Delta t}$ karena p konstan maka akibatnya $\Delta p$ sama dengan 0. Sehingga $\Sigma F = 0$

Kemudian dengan cara yang sama kita meninjau momentum angular L. Momentum angular dan impuls angular dihubungkan oleh persamaan

$\Sigma \tau \cdot \Delta t = \Delta L$ atau dapat juga ditulis menjadi $\Sigma \tau = \frac{\Delta L}{\Delta \tau}$ . Karena L konstan maka akibatnya $\Delta L$ sama dengan nol. Sehingga $\Sigma \tau = 0$ .

Akhirnya dapat disimpulkan bahwa suatu benda/sistem dikatakan setimbang jika ia memenuhi dua syarat berikut:

$\Sigma F = 0$
$\Sigma \tau = 0$

Jenis-jenis Kesetimbangan Benda Tegar

Secara umum kesetimbangan benda tegar dapat dikelompokkan menjadi dua, yakni kesetimbangan dinamis (benda yang bergerak baik secara translasi/linear ataupun secara angular dan kesetimbangan statis (benda yang betul-betul diam).

Kesetimbangan statis itu sendiri dikelompokkan menjadi 2, yaitu :

Kesetimbangan stabil, terjadi apabila suatu benda diberikan gaya maka posisinya akan berubah. Namun bila gaya tersebut dihilangkan maka posisinya akan kembali ke titik semula.
Kesetimbangan labil (tidak stabil), terjadi apabila suatu benda diberikan gaya maka posisinya akan berubah. Namun bila gaya tersebut dihilangkan maka posisinya tidak akan kembali ke titik semula.

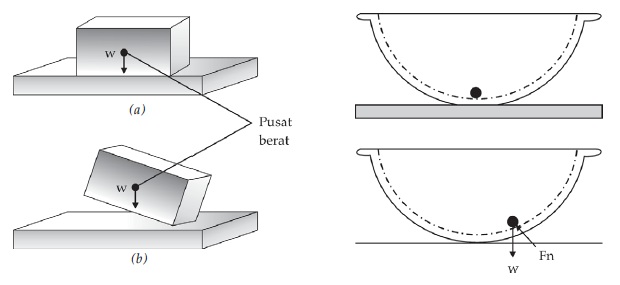
Contoh kesetimbangan stabil: kelereng di dasar mangkok ½ lingkaran. Ketika kelerang diberi gangguan (gaya) sehingga posisinya menjadi naik, namun ketika gaya tersebut dihilangkan maka posisi kelereng akan kembali ke dasar mangkok.

contoh kesetimbangan benda tegar

Sumber gambar: Dwi. S. Palupi, dkk. 2009

Sedangkan contoh kesetimbangan labil: kelereng yang diam di puncak mangkok ½ lingkaran yang terbalik. Ketika kelereng diberi gangguan sedikit, maka ia akan jatuh ke bawah, dan tidak akan kembali ke posisi semula.

kesetimbangan labil

Sumber gambar: Dwi. S. Palupi, dkk. 2009

Contoh kesetimbangan netral: kelereng yang ada di atas lantai. Ketika kelereng diberi gangguan, maka posisinya akan bergeser. Namun titik beratnya tidak akan berpindah secara vertikal.

setimbang netral

Contoh Soal :

Jika sistem pada gambar di bawah ini berada dalam keadaan setimbang, tentukan tegangan tali T₁, T₂, dan T₃. Diketahui massa beban 8 kg.

Pembahasan :
Untuk mengerjakan soal menyerupai ini, kita sanggup memakai hukum sinus sebagai diberikut :

T₁	=	T₂	=	T₃
sin a	=	sin b	=	sin c

melaluiataubersamaini :
a = sudut di hadapan T₁
b = sudut di hadapan T₂
c = sudut di hadapan T₃.

Tinjau beban :
Pada beban bekerja dua gaya yaitu gaya berat dan tegangan tali T₃. Karena dalam keadaan setimbang, maka berlaku :
∑F = 0
⇒ W - T = 0
⇒ T₃ = W
⇒ T₃ = 80 N.

melaluiataubersamaini memakai hukum sinus, maka :

T₂	=	T₃
sin b	=	sin c

T₂	=	80
sin 150	=	sin 90

T₂	=	80
½	=	1

⇒ T₂= 40 N.

Selanjutnya, diperoleh tegangan tali pertama :

T₁	=	T₃
sin a	=	sin c

T₂	=	80
sin 120	=	sin 90

T₁	=	80
½√3	=	1

⇒ T₁= 40√3 N.

Jadi, T₁= 40√3 N, T₂= 40 N, dan T₃ = 80 N.

Pada sistem kesetimbangan benda menyerupai pada gambar, AB yaitu batang sejenis dengan panjang 80 cm dan berat 20 N. Berat beban yang digantung pada ujung batang yaitu 40 N. Tentukan besar tegangan tali BC jikalau AC = 60 cm.

Pembahasan :
BC = 100 cm = 1 m.
Perhatikan gambar di atas. Tinjau batang sejenis sebagai benda yang mengalami gaya. Terdapat gaya berat balok, berat batang, dan tegangan tali dalam arah sumbu y.
∑τ = 0
⇒ W (AB) + Wb (½AB) - T sin θ (AB) = 0
⇒ 40 (0,8) + 20 (0,4) - T (⁶⁰⁄₁₀₀) (0,8) = 0
⇒ 32 + 8 - 0,48 T = 0
⇒ 0,48 T = 40
⇒ T = ⁴⁰⁄_0,48
⇒ T = 83,3 N.