Yuk Belajar Rumus Trigonometri Matematika, Lengkap Nih!

Jika anda ingin belajar tentang trigonometri sebaiknya ketahui terlebih dahulu beberapa informasi mengenai trigomoteri yang akan dijelaskan dalam artikel ini. Trigonometri berasal dari bahasa Yunani yaitu trigonon artinya tiga sudut dan metro artinya mengukur. Sehingga trigonometri adalah cabang matematika yang berhubungan dengan sudut segitiga serta fungsi trigonometri yang meliputi sinus, cosinus dan tangen.

Perlu anda ketahui bahwa trigonometri mempunyai kaitan yang erat dengan geometri sebab ada yang berpendapatan bahwa trigonometri merupakan bagian dari geometri. Meskipun begitu rumus trigonometri memiliki rumus tersendiri yang perlu anda pahami tetapi masih berkaitan dengan teori matematika lainnya.

Sebetulnya trigonometri telah bisa dilacak mulai zaman Mesir Kuno dan Babilonia serta peradaban Lembah Indus yang diperkirakan sudah berusia sekitar 3000 tahun lalu. Diketahui bahwa seorang ahli matematika India yang merintis perhitungan variable aljabar dan bisa digunakan juga untuk menghitung trigonometri dan astronomi.

Dasar dari rumus trigonometri adalah konsep kesebangunan segitiga siku-siku. Dimana sisi yang bersesuaian dari dua bangun datar yang sebangun akan mempunyai perbandingan yang sama.

Seperti teori geometri yang telah dikemukakan oleh Euclid menyatakan bahwa dari masing-masing sudut bangun datar dua segitiga mempunyai besar yang sama sehingga dua segitiga tersebut disebut sebangun. Sebab pernyataan tersebut didasarkan pada perbandingan trigonometri sudut lancip. Lalu konsep tersebut dikembangkan untuk sudut non lancip yang besarnya lebih dari 90̊ serta kurang dari nol derajat.

Fungsi Rumus Trigonometri

Selain digunakan dalam perhitungan matematika, ternyata rumus trigonometri juga bisa digunakan dalam kehidupan sehari-hari. Dimana fungsi trigonometri dalam kehidupan sehari-hari diantaranya sebagai berikut :

1. Digunakan pada teknik triangulasi dalam menghitung jarak antara bintang terdekat pada ilmu astronomi.
2. Trigonometri juga digunakan dalam geografi untuk menghitung titik tertentu serta digunakan pada sistem navigasi satelit.
3. Selain itu, trigonometri juga dipakai kriminologi dalam menghitung lintasan proyektil, memperkirakan penyebab terjadinya kecelakaan, sudut tembakan peluru, dan lain-lain.
4. Trigonometri juga dipakai dalam bidang konstruksi untuk pengukuran bidang bangunan misalnya saja pemasangan ubin, tinggi bangunan, panjang lebar, dan lain-lain.
5. Dalam dunia arsitek, trigonometri dipakai untuk menghitung beban struktural, permukaan tanah, lereng atap, dan aspek lainnya.

Dalam penggunaan trigonometri dalam kehidupan sehari-hari tersebut tentu tak bisa terlepas dari rumus trigonometri. Dimana rumus tersebut diperoleh dari bangun segitiga sama siku-siku yang dimisalkan dengan segitiga siku-siku ABC.

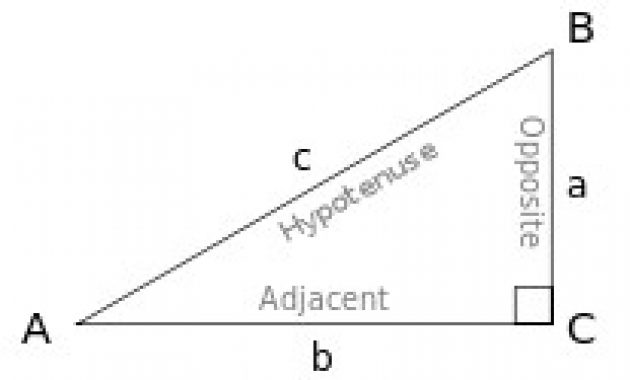
Segitiga ABC

Dimana AC dinyatakan sebagai b menjadi alas segitiga, BC dinyatakan sebagai  a yaitu tinggi atau sisi tegak segitiga. Sedangkan AB merupakan sisi miring yang dilambangkan dengan c. Dari bangun segitiga tersebut, sudut A dipakai sebagai acuannya.

Rumus Trigonometri

Sehingga untuk menghitung besar sudut atau panjang segitiga tersebut bisa dengan menggunakan rumus sebagai berikut:

Misalnya saja pada segitiga ABC, sudut A menjadi acuannya, maka untuk menentukan panjang a anda bisa memakai rumus sin A = a/c dimana besar sudut A serta panjang c telah diketahui. Sehingga dengan mengetahui besarnya sudut A serta panjang salah satu sisi dari segitiga tersebut maka anda bisa mencari panjang semua sisi segitiga tersebut termasuk pula luas dari segitiga tersebut.

Sehingga ternyata rumus trigonometri tak hanya bisa dipakai untuk rumus phytagoras saja melainkan juga dalam mencari panjang sisi segitiga.

Rumus Identitas Trigonometri

Rumus Jumlah dan Selisih Sudut Trigonometri

Rumus Perkalian Trigonometri

Rumus Jumlah dan Selisih Trigonometri

Rumus Sudut Rangkap Dua dan Tiga Trigonometri

Rumus Setengah Sudut Trigonometri

***

Itulah penjelasan mengenai rumus trigonometri yang bisa digunakan dalam kehidupan sehari-hari. Pastinya dengan rumus tersebut akan memudahkan anda dalam menyelesaikan tugas-tugas pekerjaan sebab rumus ini ternyata memiliki fungsi yang sangat banyak.