Cara Menghitung Garis Singgung Persekutuan Luar Dua Lingkaran

Masih membahas seputar garis singgung, dimana kali ini yang akan kita bahas adalah garis singgung persekutuan luar dua lingkaran.Tidak perlu berlama-lama lagi langsung saja kita bahas materi garis singgung persekutuan luar dua lingkaran ini.

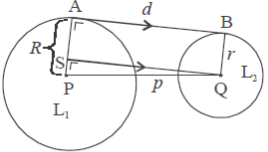
Berdasarkan gambar diatas, maka kita dapat memperoleh :

• jari-jari lingkaran yang berpusat di P = R
• jari-jari lingkaran yang berpusat di Q = r
• panjang garis singgung persekutuan luar adalah AB = d
• jarak titik pusat kedua lingakaran yaitu PQ = p

Misalnya garis AB kita geser sejajar ke bawah sejauh BQ maka diperoleh garis SQ. Selanjutnya garis AB sejajar SQ, sehingga ∠PSQ = ∠PAB = 90º (sehadap).

Kemudian perhatikan segi empat ABQS maka kita peroleh garis AB//SQ, AS//BQ, dan ∠PSQ = ∠PAB =90º. Karena segitiga PQS siku-siku di S, maka berlaku

Dikarenakan QS = AB = d, sehingga rumus panjang garis singgung persekutuan luar dua lingkaran (d) dengan jarak kedua titik pusat p, jari-jari lingkaran besar R serta jari-jari lingkaran kecil r yaitu sebagai berikut :

Agar lebih memhami materi garis singgung persekutuan luar dua lingkaran ini maka perhatikanlah contoh soal beserta pembahasannya berikut ini.

Contoh Soal.

Jika diketahui panjang garis singgung persekutuan luar dua lingkaran yaitu 12 cm, dan jarak kedua pusat lingkaran tersebut yaitu 13 cm dan panjang salah satu jari-jari lingkarannya adalah 3½ cm, maka hitunglah jari-jari lingkaran yang lain ?

Penyelesaian :

Diket :

d = 12 cm

p = 13 cm

r = 3,5 cm

Dit : R ?

Jawab :

12 = √[13² – (R – 3,5)²]

12² = 13² – (R – 3,5)²

144 = 169 – (R – 3,5)²

(R – 3,5)² = 169 -144

(R – 3,5)² = 25

R – 3,5 = √25

R – 3,5 = 5

         R = 5 + 3,5

         R = 8,5

Jadi jari-jari lingkaran yang lainnya yaitu 8,5 cm

Demikianlah materi mengenai cara menghitung garis singgung persekutuan luar dua lingkaran. Tidak sulit bukan temen-temen? Semoga setelah mempelajari artikel ini beserta contoh soalnya, temen-temen tidak merasa kesulitan ketika bertemu dengan soal serupa. Semoga bermanfaat dan Selamat Belajar.