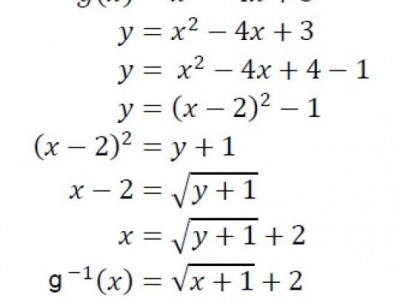Fungsi komposisi dan invers merupakan material yang masuk dalam pokok bahasan matematika di Sekolah Menengah Atas (SMA). Untuk bisa menyelesaikan masalah fungsi komposisi dan invers perlu memahami terlebih dahulu materi himpunan matematika.
Fungsi Komposisi
Dari dua jenis fungsi f(x) dan g(x) kita dapat membentuk sebuah fungsi baru dengan menggunakan sistem operasi komposisi. Operasi komposisi biasa dilambangkan dengan "o" (komposisi/bundaran). Fungsi baru yang dapat kita bentuk dari f(x) dan g(x) adalah:
(g o f)(x) artinya f dimasukkan ke g
(f o g)(x) artinya g dimasukkan ke f
Contoh:
Diketahui f(x) = 3x - 4 dan g(x) = 2x, maka tentukanlah rumus (f o g)(x) dan (g o f)(x) ...
Jawab:
(f o g)(x) = g dimasukkan ke f menggantikan x
(f o g)(x) = 3(2x)-4
(f o g)(x) = 6x - 4
(g o f)(x) = f dimasukkan ke g menggantikan x
(g o f)(x) = 2(3x-4)
(g o f)(x) = 6x-8
Ada 3 sifat fungsi komposisi:
- Tidak Komutatif
(g o f)(x) = (f o g)(x)
- Asosiatif
(f o (g o h))(x) = ((f o g) o h)(x)]
- Fungsi Identitas I(x) = x
(f o I)(x) = (I o f)(x) = f(x)
Baca Juga :
Apa Perbedaan Fungsi Injektif, Surjektif dan Bijektif ?
Pengertian Relasi, Fungsi, Domain,Kodomain dan Range
Fungsi Komposisi dan Fungsi Invers Lengkap dengan Contoh
Contoh soal lainnya:
Diketahui (f o g)(x) = x2 + 3x + 4 dan g(x) = 4x - 5. Nilai dari f(3) adalah ....
Penyelesaian:
(f o g)(x) = x2 + 3x + 4
f (g(x)) = x2 + 3x + 4
Untuk g(x) = 3 maka
4x - 5 = 3
4x = 8
x = 2
Karena f (g(x)) = x2 + 3x + 4 dan untuk g(x) = 3 didapat x = 2
Sehingga:
f (3) = 22 + 3 . 2 + 4 = 4 + 6 + 4 = 14
Fungsi Invers
Apabila fungsi dari himpunan A ke B dinyatakan dengan f, maka invers dari fungsif merupakan sebuah relasi dari himpunan A ke B. Sehingga, fungsi invers dari f: A -> B adalah f-1: B -> A.
Cara menentukan fungsi invers bila fungsi f(x) telah diketahui:
1. Ubah persamaan y = f (x) menjadi bentuk x sebagai fungsi dari y
2. Hasil perubahan bentuk x sebagai fungsiy itu dinamakan sebagai f-1(y)
3. Ubah y menjadi x [f-1(y) menjadi f-1(x)]
Fungsi Komposisi
Dari dua jenis fungsi f(x) dan g(x) kita dapat membentuk sebuah fungsi baru dengan menggunakan sistem operasi komposisi. Operasi komposisi biasa dilambangkan dengan "o" (komposisi/bundaran). Fungsi baru yang dapat kita bentuk dari f(x) dan g(x) adalah:
(g o f)(x) artinya f dimasukkan ke g
(f o g)(x) artinya g dimasukkan ke f
Contoh:
Diketahui f(x) = 3x - 4 dan g(x) = 2x, maka tentukanlah rumus (f o g)(x) dan (g o f)(x) ...
Jawab:
(f o g)(x) = g dimasukkan ke f menggantikan x
(f o g)(x) = 3(2x)-4
(f o g)(x) = 6x - 4
(g o f)(x) = f dimasukkan ke g menggantikan x
(g o f)(x) = 2(3x-4)
(g o f)(x) = 6x-8
Ada 3 sifat fungsi komposisi:
- Tidak Komutatif
(g o f)(x) = (f o g)(x)
- Asosiatif
(f o (g o h))(x) = ((f o g) o h)(x)]
- Fungsi Identitas I(x) = x
(f o I)(x) = (I o f)(x) = f(x)
Contoh soal lainnya:
Diketahui (f o g)(x) = x2 + 3x + 4 dan g(x) = 4x - 5. Nilai dari f(3) adalah ....
Penyelesaian:
(f o g)(x) = x2 + 3x + 4
f (g(x)) = x2 + 3x + 4
Untuk g(x) = 3 maka
4x - 5 = 3
4x = 8
x = 2
Karena f (g(x)) = x2 + 3x + 4 dan untuk g(x) = 3 didapat x = 2
Sehingga:
f (3) = 22 + 3 . 2 + 4 = 4 + 6 + 4 = 14 - See more at: http://www.kesekolah.com/tutorial/matematika/fungsi-komposisi-dan-invers.html#sthash.OSetWRYo.dpuf
Fungsi Komposisi
Dari dua jenis fungsi f(x) dan g(x) kita dapat membentuk sebuah fungsi baru dengan menggunakan sistem operasi komposisi. Operasi komposisi biasa dilambangkan dengan "o" (komposisi/bundaran). Fungsi baru yang dapat kita bentuk dari f(x) dan g(x) adalah:
(g o f)(x) artinya f dimasukkan ke g
(f o g)(x) artinya g dimasukkan ke f
Contoh:
Diketahui f(x) = 3x - 4 dan g(x) = 2x, maka tentukanlah rumus (f o g)(x) dan (g o f)(x) ...
Jawab:
(f o g)(x) = g dimasukkan ke f menggantikan x
(f o g)(x) = 3(2x)-4
(f o g)(x) = 6x - 4
(g o f)(x) = f dimasukkan ke g menggantikan x
(g o f)(x) = 2(3x-4)
(g o f)(x) = 6x-8
Ada 3 sifat fungsi komposisi:
- Tidak Komutatif
(g o f)(x) = (f o g)(x)
- Asosiatif
(f o (g o h))(x) = ((f o g) o h)(x)]
- Fungsi Identitas I(x) = x
(f o I)(x) = (I o f)(x) = f(x)
Contoh soal lainnya:
Diketahui (f o g)(x) = x2 + 3x + 4 dan g(x) = 4x - 5. Nilai dari f(3) adalah ....
Penyelesaian:
(f o g)(x) = x2 + 3x + 4
f (g(x)) = x2 + 3x + 4
Untuk g(x) = 3 maka
4x - 5 = 3
4x = 8
x = 2
Karena f (g(x)) = x2 + 3x + 4 dan untuk g(x) = 3 didapat x = 2
Sehingga:
f (3) = 22 + 3 . 2 + 4 = 4 + 6 + 4 = 14 - See more at: http://www.kesekolah.com/tutorial/matematika/fungsi-komposisi-dan-invers.html#sthash.OSetWRYo.dpuf
Fungsi Komposisi
Dari dua jenis fungsi f(x) dan g(x) kita dapat membentuk sebuah fungsi baru dengan menggunakan sistem operasi komposisi. Operasi komposisi biasa dilambangkan dengan "o" (komposisi/bundaran). Fungsi baru yang dapat kita bentuk dari f(x) dan g(x) adalah:
(g o f)(x) artinya f dimasukkan ke g
(f o g)(x) artinya g dimasukkan ke f
Contoh:
Diketahui f(x) = 3x - 4 dan g(x) = 2x, maka tentukanlah rumus (f o g)(x) dan (g o f)(x) ...
Jawab:
(f o g)(x) = g dimasukkan ke f menggantikan x
(f o g)(x) = 3(2x)-4
(f o g)(x) = 6x - 4
(g o f)(x) = f dimasukkan ke g menggantikan x
(g o f)(x) = 2(3x-4)
(g o f)(x) = 6x-8
Ada 3 sifat fungsi komposisi:
- Tidak Komutatif
(g o f)(x) = (f o g)(x)
- Asosiatif
(f o (g o h))(x) = ((f o g) o h)(x)]
- Fungsi Identitas I(x) = x
(f o I)(x) = (I o f)(x) = f(x)
Contoh soal lainnya:
Diketahui (f o g)(x) = x2 + 3x + 4 dan g(x) = 4x - 5. Nilai dari f(3) adalah ....
Penyelesaian:
(f o g)(x) = x2 + 3x + 4
f (g(x)) = x2 + 3x + 4
Untuk g(x) = 3 maka
4x - 5 = 3
4x = 8
x = 2
Karena f (g(x)) = x2 + 3x + 4 dan untuk g(x) = 3 didapat x = 2
Sehingga:
f (3) = 22 + 3 . 2 + 4 = 4 + 6 + 4 = 14 - See more at: http://www.kesekolah.com/tutorial/matematika/fungsi-komposisi-dan-invers.html#sthash.OSetWRYo.dpuf