Kedudukan Antara Dua Lingkaran

Kedudukan antara dua lingkaran atau kedudukan 2 lingkaran menujukkan posisi antara lingkaran pertama dan lingkaran kedua. Posisi tersebut dapat berupa lingkaran di dalam lingkaran, kedua lingkaran bersinggungan di dalam lingkaran, kedua lingkaran berpotongan di dua titik, kedua lingkaran bersinggungan di luar lingkaran, atau kedua lingkaran saling lepas (tidak memiliki titik potong). Untuk menentukan posisi lingkaran pertama terhadap lingkaran ke dua akan sangat mudah jika di lihat dalam gambar. Seperti halnya terlihat pada gambar di bawah.

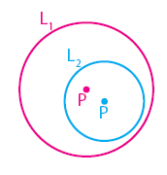
Berdasarkan gambar di atas dapat dilihat bahwa posisi lingkaran ke dua berada di dalam lingkaran pertama. Namun, bagaimana jika yang diketahui hanya persamaan kedua lingkaran? Mencari tahu kedudukan 2 lingkaran dengan menggambarnya terlebih dahulu tentu bukan merupakan solusi yang baik. Cara ini sangat tidak efektif, sehingga tidak dianjurkan. Lalu, bagaimana cara untuk mengetahui kedudukan antara dua lingkaran yang baik? Caranya dapat dilakukan dengan memanfaatkan rumus jarak antara dua titik dan kriteria yang akan dibahas pada materi di bawah. Sebelumnya, akan mari kita ingat kembali rumus mengenai jarak antara dua titik.

Jarak Titik Terhadap Garis

1. Jarak antara titik  dan .
    
   

     

2. Jarak antara titik  ke garis ax + by + c = 0.
    
   

     

Kadua rumus di atas berguna untuk menentukan jarak antara kedua pusat lingkaran. Sehingga, kedudukan 2 lingkaran dapat diketahui melalui bentuk umum persamaan lingkarannya, tanpa harus menggambarnya terlebih dahulu. Oke, sekarang mari kita simak kriteria untuk menentukan kedudukan 2 lingkaran.

Kriteria Kedudukan Antara Dua Lingkaran

Diketahui dua buah lingkaran:

1. Lingkaran 1 

   • Pusat: 

   • Jari-jari: 

2. Lingkaran 2 

   • Pusat: 

   • Jari-jari: 

Kriteria kedudukan antara dua lingkaran adalah sebagai berikut.

1. Memiliki Pusat yang Sama
   Jika  dan , maka  memiliki pusat yang sama dengan .
   

2. Bersinggungan di dalam lingkaran
   Jika , maka  dan  bersinggungan di dalam salah satu lingkaran.
   

3. Lingkaran kecil terletak di dalam lingkaran besar
   Jika , maka  di dalam .
   

4. Berpotongan di dua titik
   Jika , maka  berpotongan dengan  di dua titik.
   

5. Bersinggungan di luar lingkaran (berpotongan di satu titik)
   Jika , maka  dan  bersinggungan di luar lingkaran.
   

6. Tidak Bersinggungan (Saling Lepas)
   Jika , maka  dan  tidak bersinggugan.
   

Keterangan:  adalah jarak antara kedua pusat lingkaran. Gunakan rumus jarak antara dua titik untuk menghitung jarak kedua pusat lingkaran.

Contoh soal menentukan kedudukan dua lingkaran

Diketahui pusat lingkaran  adalah (2, 6) dengan panjang jari-jari 2 cm. Sedangkan koordinat pusat lingkaran  adalah (10, 0) dengan jari-jari 6 cm. Selidikilah kedudukan antara lingkaran  dan lingkaran !

Pembahasan:
Diketahui:

Akan dihitung jarak antara kedua titik pusat  dan 

Jumlah jari-jari adalah  cm.

Hungan antara jarak antara kedua pusat lingkaran dengan jari-jari adalah

Kriteria di atas merupakan kondisi untuk kedua lingkaran yang saling bebas (tidak berpotongan atau bersinggungan).

Jadi, hubungan antara  dan  adalah saling lepas.