Soal dan Pembahasan Peluang Majemuk Bersyarat

Soal 1.

Dua buah dadu dilemparkan bersama-sama satu kali. Peluang muncul jumlah angka kedua dadu sama dengan 3 atau 10 adalah...

Pembahasan:

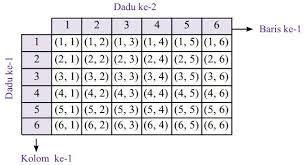
Dua kejadian pada pelemparan dua buah dadu, n(S) = 36,
A = jumlah angka = 3
B = jumlah angka = 10

Dari ruang sampel pelemparan dua buah dadu, diperoleh
A = {(1, 2), (2, 1)}
B = {(4, 6), (5, 5), (6, 4)}

n (A) = 2 → P(A) = 2/36
n (B) = 3 → P(B) = 3/36
Tidak ada yang sama antara A dan B, jadi n (A ∩B) = 0

Sehingga peluang "A atau B" adalah
P (A ∪ B) = P(A) + P(B)
= 2/36 + 3/36 
= 5/36

Soal 2.

Sebuah dadu dilemparkan satu kali. Tentukan peluang munculnya angka genap atau angka lebih besar dari 3

Pembahasan:

Ada dua kejadian, namakan kejadian A dan kejadian B dengan ruang sampel pada pelemparan satu dadu.
A = kejadian munculnya angka genap.
B = kejadian munculnya angka lebih besar dari 3.

Selengkapnya data-datanya terlebih dahulu adalah:
S = {1, 2, 3, 4, 5, 6}
n(S) = 6

A = {2, 4, 6}
n(A) = 3
maka peluang kejadian A
P (A) = n (A) / n(S) = 3 / 6

B = {4, 5, 6}
n(B) = 3
maka peluang kejadian B
P (B) = n(B) / n(S) = 3 / 6

Kelihatan ada dua angka yang sama dari A dan B yaitu angka 4 dan 6, jadikan irisannya, A ∩ B
A ∩ B = {4, 6}
n(A ∩ B) = 2
Sehingga peluang A ∩ B
P (A ∩ B) = n (A ∩ B) / n (S) = 2 / 6

Rumus peluang kejadian "A atau B"
P (A ∪ B) = P(A) + P(B) − P(A ∩ B)
= 3/6 + 3/6 − 2/6
= 4/6 = 2/3

Soal 3.

Dua dadu mata putih dan merah dilempar bersama-sama. Tentukan peluang muncul mata sama, dan berapa peluang muncul jumlah mata dadu lebih dari 10!

Pembahasan:

Diketahui :
Dua dadu mata putih dan meraj
Ditanya :
A. Peluang Muncul mata dadu sama
B. Peluang muncul jumlah mata dadu lebih dari 10

Penyelesaian :
- Kita tentukan dulu Ruang Sampelnya n(S)
n(S) = mata pada dadu x mata pada dadu
n(S) = 6 x 6
n(S) = 36

A. Muncul Mata dadu sama (n(A))
n(A) = (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)
n(A) = 6

Peluang Muncul mata dadu sama
n(P) = n(A)/n(S)
n(P) = 6/36
n(P) = 1/6

B. Muncul jumlah mata dadu kurang dari 10
n(A) = (5, 6), (6, 5), (6, 6)
n(A) = 3

Peluang Muncul Jumlah mata dadu kurang dari 10 (n(P))
n(P) = n(A) / n(S)
n(P) = 3/36
n(P) = 1/12

Soal 4.

Sebuah kantong berisi 4 bola merah, 3 bola putih, dan 3 bola hitam. Diambil sebuah bola secara acak, peluang terambil bola merah atau hitam adalah...

Pembahasan:

Jumlah semua bola yang ada dalam kantong adalah

4 + 3 + 3 = 10 bola. Dari 10 bola diambil satu bola.

A = kejadian terambil bola merah.
B = kejadian terambil bola hitam.

Bola merah ada 4, sehingga peluang terambil bola merah:
P(A) = 4/10

Bola hitam ada 3, sehingga peluang terambil bola hitam:
P(B) = 3/10

Peluang terambil bola merah atau hitam:
P(A∪B) = P(A) + P(B)
= 4/10 + 3/10
= 7/10

Soal 5.

Kotak I berisi 3 bola merah dan 2 bola putih, Kotak II berisi 3 bola hijau dan 5 bola biru. Dari masing – masing kotak diambil 2 bola sekaligus secara acak. Peluang terambilnya 2 bola merah dari kotak I dan 2 bola biru dari kotak II?

Pembahasan:

Peluang 2 bola merah pada Kotak I :

P(A) =

    =

    =

    =

Peluang 2 bola biru pada Kotak I :

P(A) =

    =

    =

    =

Peluang terambilnya 2 bola merah dari kotak I dan 2 bola biru dari kotak II adalah

   = 3/10 x 10/28

   = 3/28