Cara Menghitung Relasi dan Fungsi Beserta Contoh Soal

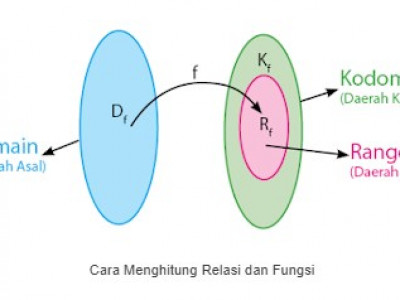
Relasi dan fungsi merupakan materi dalam ilmu Matematika yang dipelajari ketika berada dibangku sekolah tingkat menengah atas. Dalam menghitung relasi dan fungsi tersebut dapat dilakukan dengan beberapa cara. Lau bagaimana cara menyelesaikan soal soal relasi dan fungsi Matematika? Nah pada kesempatan kali ini saya akan menjelaskan tentang cara menghitung relasi dan cara menghitung fungsi beserta contoh soal relasi dan contoh soal fungsi. Untuk lebih jelasnya dapat anda simak di bawah ini.

Pengertian relasi secara sederhana ialah hubungan. Relasi tersebut menghubungkan domain (daerah asal) dengan kodomain (daerah kawan). Sedangkan pengertian fungsi ialah relasi yang menghubungkan tepat satu himpunan anggota pada daerah asal ke himpunan anggota daerah kawan. Relasi dan fungsi pada Matematika tersebut berbeda, mulai dari cara menghitung relasi dan cara menghitung fungsi hingga contoh soal relasi dan contoh soal fungsi. Selain itu adapula perbedaan lain yaitu cara pemasangan himpunan anggota pada daerah asalnya.

Baca Juga :

Pengertian Relasi, Fungsi, Domain,Kodomain dan Range

Gambar diatas menunjukan perbedaan jelas antara relasi dan fungsi. Dalam pemasangan setiap anggota relasi pada daerah asal ke daerah kawan tidak memiliki aturan khusus. Bahkan dalam relasi tersebut terdapat anggota asal yang boleh tidak memiliki pasangan ataupun memiliki pasangan yang lebih dari satu. Sedangkan untuk pemasangan setiap anggota fungsi pada daerah asal ke daerah kawan memiliki aturan khusus. Fungsi tersebut mengharuskan setiap anggota asalnya memiliki pasangan hanya satu pada daerah kawan. Maka dari tu dapat disimpulkan bahwa setiap fungsi pasti termasuk dalam relasi, sedangkan setiap relasi belum tentu termasuk fungsi. Di bawah ini terdapat penjelasan lebih lanjut mengenai cara menghitung relasi dan cara menghitung fungsi beserta contoh soal relasi dan contoh soal fungsi.

Relasi

Relasi ialah pernyataan yang berisi hubungan antara anggota suatu himpunan dengan anggota satu himpunan lain. Maka dari itu setiap anggota yang saling berpasangan akan dinyatakan dalam bentuk relasi himpunan A dan himpunan B. Cara menghitung relasi tersebut dapat dilakukan dengan beberapa cara yaitu melalui diagram Cartesius, diagram panah dan himpunan pasangan berurutan.

Diagram Panah

Cara menghitung relasi yang pertama ialah melalui diagram panah. Diagram panah tersebut merupakan cara menyatakan sebuah relasi yang cukup mudah dilakukan. Relasi yang dinyatakan dalam bentuk diagram ini ditunjukkan dengan gambar anak panah dari anggota himpunan A ke anggota himpunan B. Untuk lebih jelasnya dapat anda perhatikan contoh soal relasi dibawah ini:

Disebuah kelas terdapat empat anak yang diminta untuk menyebutkan warna kesukaannya. Anak tersebut bernama Gita, Wahyu, Tina dan Riski. Warna kesukaan Gita ialah biru, warna kesukaan Wahyu ialah hitam, warna kesukaan Tina ialah hijau dan warna kesukaan Riski ialah biru. Dalam pernyataan ini terdapat dua himpunan yaitu himpunan anak (A) dan himpunan warna kesukaan (B). Jika relasi pada kedua himpunan ini dibentuk dalam diagram panah, maka akan menjadi seperti dibawah ini:

Kedua himpunan (himpunan A dan himpunan B) tersebut saling berpasangan pada setiap anggotanya dengan dinyatakan dalam bentuk panah seperti gambar diagram di atas. Maka dari itu cara menghitung relasi dapat menggunakan diagram panah seperti di atas.

Himpunan Pasangan Berurutan

Cara menghitung relasi selanjutnya dapat menggunakan himpunan pasangan berurutan. Himpunan pasangan berurutan ini dapat menyatakan relasi himpunan A yang dipasangkan secara berurutan dengan himpunan B. Pernyataan relasi ini menerapkan himpunan berurutan (x,y) dimana x ∈ A dan y ∈ B. Untuk lebih jelasnya dapat anda simak contoh soal relasi dibawah ini:

Disebuah kelas terdapat empat anak yang diminta untuk menyebutkan warna kesukaannya. Anak tersebut bernama Gita, Wahyu, Tina dan Riski. Warna kesukaan Gita ialah biru, warna kesukaan Wahyu ialah hitam, warna kesukaan Tina ialah hijau dan warna kesukaan Riski ialah biru. Jika relasi pada kedua himpunan ini dibentuk dalam himpunan pasangan berurutan, maka akan menjadi seperti dibawah ini:

(Gita, biru), (Wahyu, hitam), (Tina, hijau), (Riski, biru).

Diagram Cartesius

Cara menghitung relasi selanjutnya dapat menggunakan diagram cartesius. Diagram Cartesius ini dapat menyatakan relasi himpunan A dengan himpunan B dalam bentuk titik titik (dot). Untuk lebih jelasnya dapat anda simak contoh soal relasi dibawah ini:

Himpunan A = {Gita, Wahyu, Tina, Riski} dan himpunan B = {biru, hitam, hijau}. Kedua himpunan ini dapat dinyatakan sebagai relasi menggunakan diagram cartesius seperti gambar berikut:

Fungsi

Fungsi atau pemetaan ialah relasi setiap anggota himpunan A yang berpasangan dengan anggota himpunan B. Anggota yang terdapat pada himpunan A dinamakan Domain atau daerah asal. Sedangkan anggota yang terdapat pada himounan B dinamakan Kodomain atau daerah kawan. Kemudian adapula istilah Range yang merupakan hasil pemetaan pada daerah asal dengan daerah kawan. Cara menghitung fungsi dapat dilakukan dengan diagram panah, diagram cartesius maupun melalui himpunan pasangan berurutan. Perhatikan diagram panah pada fungsi di bawah ini:

Berdasarkan fungsi diagram panah diatas dapat kita simpulkan bahwa:
Domain A = {1, 2}
Kodomain B = {1, 2, 3}
Range fungsi = (1, 3)

Fungsi dalam ilmu Matematika ini dapat dinyatakan dalam bentuk huruf kecil seperti f, g, ataupun h. Contohnya fungsi f memetakan himpunan A ke himpunan B, maka dapat ditulis menjadi f(x) dimana mempunyai aturan f : x → 2x + 2. Artinya x dipetakan oleh fungsi f menjadi 2x + 2. Maka dari itu fungsi f mempunyai daerah bayangan x yaitu 2x + 2 sehingga dapat dijabarkan menjadi f(x) = 2x + 2. Cara menghitung fungsi tersebut menerapkan rumus fungsif yaitu f(x) = ax + b atau fungsi f : x → ax +b, dimana x adalah anggota domain dari f. Untuk lebih jelasnya dapat anda simak contoh soal fungsi di bawah ini:

Diketahui fungsi f : x → 2x + 2 pada himpunan bilangan bulat. Hitunglah:
1. f(5)
2. bayangan (-3) oleh f
3. nilai f untuk x = 7
4. nilai x untuk f(x) = 8
5. nilai a jika f(a) = 16

Jawab.
Fungsi f : x → 2x + 2
Rumus fungsi: f(x) = 2x + 2

1. f(5) = 2 (5) + 2 = 10

2. bayangan (-3) oleh f

    f(-3) = 2 (-3) + 2 = -4

3. nilai f untuk x = 7

    f(7) = 2 (7) + 2 = 16

4. nilai x untuk f(x) = 8

        f(x) = 8

    2x + 2 = 8

          2x = 8 - 2

          2x = 6

            x = 3

5. nilai a jika f(a) = 16

        f(a) = 16

    2a + 2 = 16

          2a = 16 - 2

          2a = 14

            a = 7

Sekian penjelasan mengenai cara menghitung relasi dan cara menghitung fungsi beserta contoh soal relasi dan contoh soal fungsi. Setiap fungsi pasti termasuk dalam relasi, sedangkan setiap relasi belum tentu termasuk fungsi. Semoga artikel ini dapat bermanfaat. Terima kasih.

Baca Juga : Pengertian Fungsi dan Macam-macam Fungsi dalam Matematika

6. Jelaskan cara menentukan rumus fungsi jika diketahui fungsi f  dinyatakan oleh f(x) = ax + b , f(-1) = 2, f(2) = 11.

Jawab :

f(x) = ax + b = f(-1) = a(-1) + b

                          2   = a(-1) + b

                          2   = -1a + b .......................(pers 1)

f(2) = a(2) + b

   11= a(2) + b

  11 = 2a + b..........................(pers 2)

Dengan menggunakan substitusi

2 = -1a + b

b = 2 + 1a ...........(pers 3)

Substitusikan persamaan (3) ke persamaan (2)

11 = 2a + b

11 = 2a + 2 + 1a

11 – 2 = 3a

     9    = 3a

     a    = 3

Mencari nilai b dari persamaan 3

b = 2 + 1a

= 2 + 1 . 3

= 2 + 3

= 5

Jadi rumus fungsi f(x) = ax + b = 3x + 5

7. Fungsi f ditentukan oleh f(x) = ax + b, jika f(4) = 5, f(-2) = -7

1. Tentukanlah nilai a dan b
2. Persamaan fungsi tersebut

Jawab :

a. f(x) = ax + b = f(4) = a(4) + b

                               5 = a(4) + b

                               5 = 4a + b .......................(pers 1)

b. f(-2) = a(-2) + b

       -7 = a(-2) + b

       -7 = -2a + b..........................(pers 2)

Dengan menggunakan substitusi

5 = 4a + b

b = 5 - 4a ...........(pers 3)

Substitusikan persamaan (3) ke persamaan (2)

-7 = -2a + b

-7 = -2a + (5 - 4a)

-7 – 5 = -6a

- 12 = -3a

   a  = 4

Mencari nilai b dari persamaan 3

b = 5 - 4a

   = 5 - 4 . 4

   = 5 - 16

   = -9

Jadi rumus fungsi f(x) = ax + b = 4x – 9

8. Diketuhui fungsi f(x) = ax + b, f(2) = -2, f(3) = 13. Tentukan nilai f(4)

Jawab :

a. f(x) = ax + b =  f(2) = a(2) + b

                              -2 = a(2) + b

                              -2 = 2a + b .......................(pers 1)

    f (3) = a(3) + b

      13 = a(3) + b

      13 = 3a + b..........................(pers 2)

Dengan menggunakan substitusi

-2 = 2a + b

b = -2 - 2a ...........(pers 3)

Substitusikan persamaan (3) ke persamaan (2)

13 = 3a + b

13 = 3a + (-2 - 2a)

13 + 2 = a

15 = a

Mencari nilai b dari persamaan 3

b = -2 - 2a

   = -2 - 2 . 15

   = -2 - 30

   = -32

rumus fungsi f(x) = ax + b = 15x – 32

                       f(4) = 15.(4) – 32

                             = 60 – 32

                             = 28