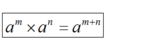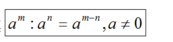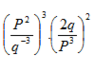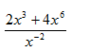Sifat Bilangan Berpangkat Beserta Pengertiannya Dalam Matematika

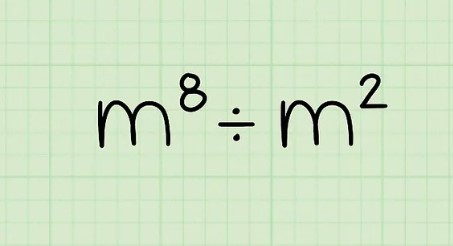
Bilangan berpangkat merupakan salah satu cabang ilmu matematis yang dipelajari sejak kita duduk di bangku Sekolah Dasar . Dan merupakan bentuk kelanjutan dari operasi hitung yang terdiri dari penjumlahan , pengurangan , pembagian dan perkalian .

Sebelum kita mempelajari bilangan berpangkat lebih dalam , maka kita harus mengetahui terlebih dahulu pengertian dari bilangan berpangkat itu sendiri , baru kita mempelajari jenis dan sifat – sifat dari bilangan berpangkat .

Pengertian Dan sifat Bilangan Berpangkat

A. Pengertian bilangan berpangkat 

Bilangan berpangkat , yaitu merupakan bilangan penyederhana dari sebuah bilangan yang di kalikan , atau untuk lebih memahaminya perhatikan penjelasan di bawah ini :

aⁿ  = a x a x a x a x . . . .x n ( Sebanyak n )

Keterangan :

aⁿ = bilangan berpangkat

a = bilangan pokok

n = pangkat

B. Jenis – Jenis Bilangan Berpangkat

Bilangan berpangkat , terdiri dari beberapa jenis yaitu :

1. Bilangan berpangkat bulat positif 

yaitu merupakan penyederhanaan dari seatu perkalian bilangan bulat yang memiliki faktor yang sama .

Apabila dirumuskan adalah :

aⁿ  = a x a x a x a x . . . .x n ( Sebanyak n )

Ket:

a = bilangan dasar ( bilangan pokok )

n = pangkat  ( eksponen )

Contoh :

2⁵ = 2 x 2 x 2 x 2 x 2 = 32

7² = 7 x 7 = 49

2. Bilangan Berpangkat bulat negatif

Yaitu merupakan bilangan yang pangkatnya merupakan bilangan negatif .

Apabila dirumuskan :

Contoh :

10^-2  =  1 / 10² 

3. Bilangan Berpangkat Nol

Yaitu merupakan bilangan berpangkat yang pangkatnya nol . Dan semua bilangan yang di pangkatkan nol hasilnya 1.

Apabila dirumuskan :

a⁰ = 1

C. Sifat – sifat Bilangan Berpangkat

Untuk dapat megerjakan permasalahan – permasalahan di dalam soal bilangan berpangkat , kita harus mengetahui sifat – sifat bilangan berpangkat supaya kita dalam mengerjakannya kita memiliki tata aturan dasar atau sebagai pacuan dalam mengerjakannya dan supaya mempermudah dalam mengerjakannya .

Sifat – sifat bilangan berpangkat adalah sebagai berikut :

1. Perkalian Bilangan Berpangkat 

Dalam perkalian bilangan berpangkat , maka berlaku sifat seperti di bawah ini :

Contoh :

• 2² x 2⁶ = 2 ²⁺⁶  = 2⁸
• 3² x 3² = 2 ²⁺²  = 2⁴

2. Pembagian Bilangan Berpangkat 

Dalam pembagian bilangan berpangkat berlaku rumus :

Contoh :

• 3⁶ : 3² = 2 ^6-2  = 2⁴
• 6⁶ : 6³ = 6^6-3 = 6³

3. Sifat Pemangkatan Bilangan Berpangkat 

Apabila ada suatu bilangan berpagkat yang di pangkatkan lagi ,maka berlaku rumus :

(a^m)ⁿ  =  a ^{m x n}

Contoh :

( 2³ ) ²  = 2 ^{3 x 2}  = 2⁶

4. Sifat Perpangkatan Suatu Perkalian atau pembagian 

• Apabila ada dua bilangan bulat yang dikalikan dan di pangkatkan maka berlaku rumus :

 ( a x b ) ⁿ = aⁿ  x bⁿ

• Apabila ada dua bilangan bulat yang di bagi dan di pangkatkan maka berlaku rumus :

( a : b ) ⁿ = aⁿ  : bⁿ

Contoh Soal 

1. Sederhanakan bentuk bilangan berpangkat berikut :

 a. 

b. 

Penyelesaian :

a. 

< = >(  P⁶ / q ^-9 ) ( 4q² /p⁶ )

< = >(  P⁶ : 1/ q ⁹ )   (4q² . p-⁶ )

< = > (P⁶ . q ⁹ ) (4q² . p-⁶ )

< = > 4. P^{6 + (-6)} . q ⁹⁺²

<= > 4. P⁰ . q ¹¹

< = > 4.1. q ¹¹

< = > 4 q ¹¹

b. 

< = > 2x³ : x ^-2  + 4x⁶ : x ^-2

< = > 2x³ : 1/ x² + 4x⁶ : 1/ x²

< = > 2x³ .  x²  + 4x⁶  . x ²

< = > 2 x^{3 + 2}  + 4 x^{6 + 2}

< = > 2 x⁵ + 4x⁸

2. Tentukan hasil dari bentuk pangkat berikut :

a. 5³ x 5⁴

b. ( -3 ) ⁶ x ( -3 ) ⁹

c. ( – 2 ) ¹⁰ x ( -2 ) ²⁰

d. a¹⁰ x a²⁰ x a³⁰

Penyelesaian :

a. 5³x 5⁴ = 5 ^{3+ 4}  = 5⁷

b. ( -3 )⁶x ( -3 )⁹  = ( – 3 ) ^{6 + 9}  = ( – 3 ) ¹⁵

c. ( – 2 )¹⁰x ( -2 ) ²⁰ = ( -2 ) ^{10 + 20}  = ( -2 ) ³⁰

d. a¹⁰x a²⁰x a³⁰  = a ^{10 + 20 + 30}  = a ⁶⁰

Demikian penjelasan mengenai materi ini. Intinya , dalam bilangan berpangkat , ada hubungan antara penjumlahan , pengurangan , perkalian dan pembagian . Dan supaya dalam mengerjakan soal bilangan berpangkat menjadi lebih mudah , maka anda semua harus memahami betul mengenai sifat – sifat bilangan berpangkat . Jika anda sudah memahaminya , maka di buat dalam bentuk apa pun akan terasa mudah . Semoga dengan penjelasan dan contoh di atas , kita semua akan bertambah ilmunya . Serta dapat membantu permasalahan dalam materi bilangan berpangkat .