Rumus Peluang dan Contoh-contoh Soalnya

Rumus peluang adalah P(A) = n(A)/n(S), yaitu pembagian jumlah ruang sampel dengan jumlah ruang semesta kejadian peristiwa. Membahas mengenai peluang tidak terlepas dari percobaan, ruang sampel, dan kejadian.

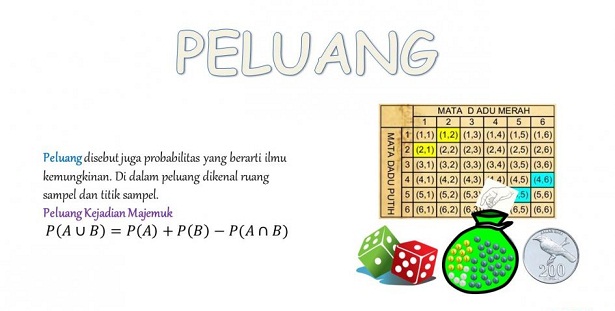
Percobaan (eksperimen) dalam peluang digunakan untuk mendapatkan hasil kemungkinan yang terjadi selama percobaan tersebut berlangsung dan hasil tersebut tidak dapat ditentukan atau diramalkan. Percobaan sederhana mengenai peluang yaitu menghitung peluang dadu, mata uang.

Ruang sampel merupakan himpunan dari semua hasil yang mungkin pada suatu percobaan. Dalam persamaan, ruang sampel biasanya disimbolkan dengan lambang S.

Baca Juga :

Kombinasi Pada Peluang dan Contohnya

Menentukan Peluang Kejadian Majemuk Dan Kejadian Bersyarat

Kejadian atau peristiwa adalah himpunan bagian dari ruang sampel atau bagian hasil percobaan yang diinginkan. Kejadian dapat berupa kejadian tunggal (hanya memiliki satu titik sampel) dan kejadian majemuk (memiliki lebih dari satu titik sampel).

Berdasarkan jabaran definisi percobaan, ruang sampel, dan kejadian. Maka, dapat didefinisikan peluang adalah kemungkinan atau kebolehjadian pada suatu peristiwa pada ruang sampel tertentu dalam suatu percobaan.

“Peluang atau kebolehjadian atau bisa disebut probabilitas adalah cara untuk mengungkapkan kepercayaan atau pengetahuan bahwa suatu kejadian akan berlaku atau telah terjadi”

Peluang atau probabilitas suatu kejadian adalah angka yang menunjukkan kemungkinan suatu kejadian. Nilai peluang berada pada kisaran antara 0 dan 1.

Kejadian dengan nilai probabilitas 1 merupakan kejadian yang pasti atau telah terjadi. Contoh dari kejadian probabilitas 1 yaitu matahari pasti muncul waktu siang hari, bukan malam hari.

Suatu kejadian yang mempunyai nilai probabilitas 0 merupakan kejadian mustahil atau tidak mungkin terjadi. Contoh dari kejadian probabilitas 0 yaitu misal sepasang kambing melahirkan seekor sapi.

Daftar Isi

Rumus Peluang

Probabilitas/Peluang suatu kejadian A terjadi dilambangkan dengan notasi P(A), p(A), atau Pr(A). Sebaliknya, probabilitas [bukan A] atau komplemen A, atau probabilitas suatu kejadian A tidak akan terjadi, adalah 1-P(A).

Untuk menentukan rumus peluang kejadian menggunakan ruang sampel (biasanya disimbolkan dengan S) dan suatu kejadian. Jika A adalah suatu kejadian atau peristiwa, maka A adalah anggota dari himpunan ruang sampel S. Peluang kejadian A adalah:

P(A) = n(A)/ n(S)

Keterangan:
N(A) = banyak anggota himpunan kejadian A
n(S) = banyak anggota dalam himpunan ruang sampel S

Contoh Soal Rumus Peluang

Contoh Soal 1:

Sebuah dadu dilempar satu kali. Tentukan peluang ketika:

a. Kejadian A munculnya mata dadu dengan angka prima

b. Kejadian munculnya mata dadu dengan jumlah kurang dari 6

Jawab:

Percobaan melempar dadu menghasilkan 6 kemungkinan yaitu munculnya mata dadu 1, 2, 3, 4, 5, 6, sehinga dapat dituliskan bahwa n (S)= 6

a. Pada pertanyaan munculnya mata dadu prima, yaitu peristiwa angka yang muncul merupakan bilangan prima, yaitu 2, 3, dan 5. Sehingga dapat dituliskan jumlah kejadian n(A) = 3.

Jadi nilai peluang dari kejadian A tersebut adalah sebagai berikut:

P(A) = n(A)/ n(S)

P(A) = 3/6 = 0,5

b. Pada kejadian B, yaitu peristiwa muncul mata dadu dengan jumlah kurang dari 6. Kemungkinan angka yang muncul yaitu 1, 2, 3, 4, dan 5.

Jadi nilai peluang dari kejadian B tersebut adalah sebagai berikut:

P(B) = n(B)/ n(S)

P(A) = 5/6

Contoh Soal 2

Tiga mata uang logam dilempar bersama. Tentukan peluang muncul dua sisi gambar dan satu sisi angka.

Jawab:

Ruang sampel untuk pelemparan 3 mata uang logam:

S = {GGG, GGA, GAG, AGG, AGA, GAA, AAA, AAG}

maka n(S) = 8

*untuk mencari nilai n(S) pada satu kali pelemparan 3 logam uang yaitu dengan n(S) = 2^n (dengan n adalah jumlah mata uang logam, atau jumlah pelemparan)

Kejadian muncul dua mata sisi gambar dan satu sisi angka yaitu:

N(A) {GGA, GAG, AGG},

maka n(A) = 3

Jadi, peluang untuk memperoleh dua sisi gambar dan satu angka adalah berikut:

P(A) = n(A)/ n(S) = 3/8

Contoh Soal 3

Tiga bola lampu dipilih secara acak dari 12 bola lampu yang 4 diantaranya rusak. Carilah peluang kejadian munculnya:

1. Tidak ada bola lampu yang rusak
2. Tepat satu bola lampu yang rusak

Jawab:

Untuk memilih 3 bola lampu dari 12 lampu yaitu:

12C3 = (12)! / 3! (12-3)!

= 12! / 3! 9!

= 12 x 11 x 10 x 9!/ 1 x 2 x 3 x 9!

= 12 x 11 x 10 / 1 x 2 x 3 = 220

Sehingga, n(S) = 220

Misalkan kejadian A untuk kasus tidak ada bola yang rusak. Karena ada 12 – 4 = 8 , yaitu 8 banyaknya jumlah lampu yang tidak rusak, maka untuk memilih 3 bola lampu tidak ada yang rusak yaitu:

8C3 = 8!/ (8-3)! 3!

= 8 x 7 x 6 x 5!/ 5! 3 x 2 x 1

= 56 cara

Sehingga, n (A) = 56 cara

Maka untuk menghitung peluang kejadian tidak ada lampu yang rusak yaitu:

P(A) = n(A) //n(S)

= 56/ 220 = 14/55

Misalkan kejadian B yaitu munculnya tepat satu bola yang rusak, maka terdapat 4 bola lampu yang rusak. Jumlah bola yang diambil ada 3 buah, dan satu diantaranya tepat rusak, sehingga 2 yang lainnya merupakan bola lampu yang tidak rusak.

Dari kejadian B tersebut didapatkan cara untuk mendapat 1 bola yang rusak dari 3 bola yang diambil.

8C2 = 8 x 7 x 6!/ (8-2)! 2×1

=8 x 7 x 6!/ 6! 2

=28

Terdapat 28 cara untuk untuk mendapat 1 bola yang rusak, dimana dalam satu kantong terdapat 4 buah lampu yang rusak. Sehingga banyak cara untuk mendapat tepat satu bola yang rusak dari 3 bola yang diambil adalah:

n(B) = 4 x 28 cara = 112 cara

Jadi dengan rumus peluang kejadian, munculnya tepat satu bola lampu yang rusak adalah

P(B) = n(B) /n(S)

= 112/ 220

= 28/55

Contoh Soal 4

Dua kartu diambil dari 52 kartu. carilah peluang terjadinya (a) kejaidan A : kedua kartu sekop, (b) Kejadian B: satu sekop dan satu hati

Jawab:

Untuk mengambil 2 kartu dari 52 kartu yang ada:

53C2 = 52 x 51/ 2 x 1 = 1.326 cara

Sehingga n(S) = 1.326

• Kejadian A

Untuk mengambil 2 sekop dari 13 sekop ada:

13C2 = 13 x 12 / 2 x 1

=78 cara

sehingga n(A) = 78

Maka peluang kejadian A adalah

P(A) = n(A)/n(S)

=78/1.326

=3/51

Jadi peluang kedua kartu terambil adalah sekop, maka peluangnya adalah 3/51

• Kejadian B

Karena terdapat 13 sekop dalam 13 hati, maka untuk mengambil sebuah kartu sekop dan satu hati ada beberapa cara:

13 x 13 = 69 cara , n(B) = 69

Maka peluang nya:

P(B) = n(B)/ n(S)

=69/1.326

=13/102

Jadi peluang mengambil dua kartu dengan satu sekop dan satu hati, nilai peluang yang muncul adalah 13/102.