Rumus Hukum Kirchoff I dan II

Hukum Kirchhoff ialah merupakan dua persamaan yang saling berhubungan dengan arus namun berbeda potensial (umumnya dikenal dengan tegangan) dalam rangkaian listrik. Pertama kali Hukum ini diperkenalkan yakni oleh seorang ahli fisika Jerman yang bernama Gustav Robert Kirchhoff (1824-1887) pada tahun 1845.

contoh hukum kirchoff

Tegangan jatuh pada  dan  tidaklah sama karena adanya ggl . Sehingga, rangkaian kedua resistor ini tidaklah paralel juga bukanlah rangkaian seri, karena arus yang mengalir pada kedua resistor tidaklah sama. Namun, ada hukum yang berlaku pada rangkaian yang memliki arus tetap (tunak). Hukum ini adalah hukum Kirchhoff 1 dan 2.

Hukum Kirchoff 1

Pengertian Hukum Kirchoff Satu (1)

Hukum Kirchhoff 1 yaitu Hukum Kirchhoff yang selalu berkaitan dengan arah arus yang menghadapi titik percabangan. Kemudian Hukum Kirchhoff 1 ini sering juga disebut dengan Hukum Arus Kirchhoff atau Kirchhoff’s Current Law (KCL).

Bunyi Hukum Kirchhoff 1

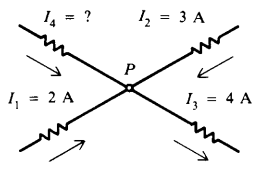
“Arus Total yang masuk melalui suatu titik percabangan pada suatu rangkaian listrik sama dengan arus total yang keluar dari titik percabangan tersebut.”

Rumus Hukum Kirchoff satu (1)

Untuk lebih jelasnya mengenai Bunyi Hukum Kicrhhoff 1
Lihat rumus dan rangkaian sederhana dibawah ini :

Berdasarkan Rangkaian diatas, dirumuskan bahwa :

Hukum Kirchoff 2

Pengertian Hukum Kirchoff Dua (2)

Hukum Kirchhoff 2 yaitu hukum yang dipakai untuk menganalisis tegangan (beda potensial) komponen-komponen elektronika pada suatu rangkaian tertutup. Pada Hukum Kirchhoff 2 ini jufa pada umumnya dikenal dengan sebutan Hukum Tegangan Kirchhoff atau Kirchhoff’s Voltage Law(KVL).

Bunyi Hukum Kirchhoff 2

“Total Tegangan (beda energi potensial) pada suatu rangkaian tertutup adalah nol”

Rumus Hukum Kirchoff Dua (2)

rumus

Untuk lebih jelas mengenai Bunyi Hukum Kirchhoff 2Hukum Kirchhoff 2
Lihat rumus dan rangkaian sederhana berikut :

Berdasarkan Rangkaian tersebut, dirumuskan bahwa :