Persamaan Dan Pertidaksamaan Trigonometri

Sekarang ini yang akan kita pelajari mengenai persamaan dan pertidaksamaan dalam trigonometri. Artikel ini bertujuan untuk memudahkan sobat semua dalam belajar matematika sehingga ketika menemui soal mengenai persamaan ataupun pertidaksamaan trigonometri tidak akan merasa kesulitan.

Persamaan Dasar

sin x = sin a                  

x = a + k.360° atau x = (180 – a) + k.360° (kuadran I atau II)

cos x = cos a

x = a + k.360° atau x = –a + k.360° (kuadran I atau IV)

tan x = tan a

x = a + k.180

dalam hal ini k = bilangan bulat merupakan bilangan yang terdiri dari bilangan cacah dan negatifnya. Yang termasuk dalam bilangan cacah yaitu 0,1,2,3,4,… sehingga negatif dari bilangan cacah yaitu -1,-2,-3,-4,… dalam hal ini -0 = 0 maka tidak dimasukkan lagi secara terpisah.

Notes :

Jika tedapat persamaan cos x = sin a, cot x = tan a, sec x = cosec a, atau sebaliknya, salah satu diubah menjadi (90 – a)°. Misalnya : cos x = sin a → cos x = cos (90 – a)°

Baca Juga :

Pengertian Trigonometri dan Rumus Trigonometri Lengkap dengan Soal

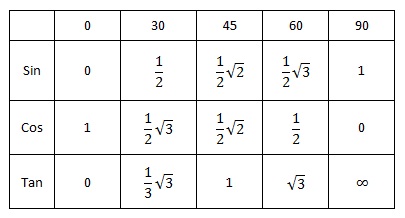
Perbandingan Trigonometri dan Tabel Trigonometri Lengkap

Perhatikan contoh berikut :

1.Tentukan HP (Himpunan Penyelesaian) dari 2 cos x – √3 = 0 untuk 0 ≤ x ≤ 360°

Jawab :

2 cos x = √3

cos x = ½ √3

cos x = cos 30°

x = 30° + k.360°              atau                        x = (180 – 30)° + k.360°

k = 0 → x = 30°                                                 x = 150° + k.360°

k = 1 → x = 390° (tidak memenuhi)         k = 0 → x = 150°

Sehingga HP = {30°, 150°}

 

2.Tentukan HP dari tan (60 – ½ x)° = cot (x + 120)° untuk 0 ≤ x ≤ 360°

tan (60 – ½ x)° = tan (90 – (x + 120))°

tan (60 – ½ x)° = tan (–x – 30)°

60° – ½ x = –x – 30° + k.180°

x – ½ x = –30° – 60° + k.180°

½ x = –90° + k.180°

x = –180° + k.360°

k = 1 → x = 180°

Sehingga  HP = {180°}

Persamaan Bentuk A Cos Nx + B Sin Nx

Jika kita menemukan persamaan dalam bentuk a cos nx + b sin nx maka kita ubah menjadi k cos(nx – α)

dimana

Kemudian  diselesaikan seperti menyelesaikan persamaan dasar cos x = cos a

Penentuan letak α:

• Jika a +, b + → α di kuadran I
• Jika a –, b + → α di kuadran II
• Jika a –, b – → α di kuadran III
• Jika a +, b – → α di kuadran IV

Untuk persamaan a cos nx + b sin nx = c,

syarat agar persamaan ini dapat diselesaikan:

Dan persamaan ini tidak dapat diselesaiakan jika :

Persamaan Bentuk A Cos²x + B Sin X.Cos X + C Sin²x = D

Ketika terdapat bentuk persamaan a cos²x + b sin x.cos x + c sin²x = d. Untuk menyelesaikannya lakukan dengan mengubah unsur-unsurnya seperti berikut ini:

Dan untuk berikutnya persamaan diselesaikan seperti halnya menyelesaikan persamaan a cos nx + b sin nx = c

 

Persamaan Berbentuk A(Cos X ± Sin X) + B Sin X.Cos X + C = 0

Untuk persamaan berbentuk a(cos x ± sin x) + b sin x.cos x + c = 0, dalam menyelesaikannya kita dapat mengikuti cara sebagai berikut :

Misalnya (cos x ± sin x) = p

sehingga

(cos x ± sin x)² = p²

cos²x ± 2 sin x.cos x + sin²x = p²

1 ± 2 sin x.cos x = p²

± 2 sin x.cos x = p² – 1

Sehingga 2 sin x.cos x = ± ½ (p² – 1)

Sehingga persamaan di atas akan menjadi persamaan kuadrat:

a.p ± ½ b(p² – 1) + c = 0

Selesaikan dengan cara pemfaktoran atau rumus abc untuk mendapatkan nilai p, selanjutnya persamaan cos x ± sin x = p dapat diselesaikan dengan cara ketika menyelesaikan persamaan a cos nx + b sin nx = c

 

Nilai Ekstrim Y = A Cos Nx + B Sin Nx + C

Pertidaksamaan Trigonometri

Langkah yang dilakukan dalam menyelesaikan pertidaksamaan trigonometri pada hakikatnya hampir sama dalam menyelesaikan persamaan trigonometri. Hanya terdapat tambahan menentukan daerah penyelesaian. Berikut ini langkah-langkahnya :

1. Mencari harga nol sama dengan cara menyelesaikan persamaan trigonometri

2. Diselesaikan dengan menggunakan garis bilangan

Contoh:

Selesaikan sin 2x < cos x  untuk 0 ≤ x ≤ 360°

Penyelesaian :

sin 2x – cos x < 0

2 sin x.cos x – cos x < 0

cos x.(2 sin x – 1) < 0

harga nol:

• cos x = 0

cos x = cos 90°

x = 90° + k.360°      atau      x = –90° + k.360°

k = 0 → x = 90°                        k = 1 → x = 270°

• 2 sin x – 1 = 0

2 sin x = 1

sin x = ½

sin x = sin 30°

x = 30° + k.360°        atau      x = (180 – 30)° + k.360°

k = 0 → x = 30°                         x = 150° + k.360°

k = 0 → x = 150°

Memberi tanda (+) dan (-) pada garis bilangan:

Jika x = 180° maka sin 2.180° – cos 180° = sin 360° – cos 180° = 0 – (–1) = 1 (+)

Jadi garis bilangannya sebagai berikut:

berdasarkan soal yang diminta yaitu kurang dari (<) 0, maka yang diarsir adalah bagian-bagian yang bertanda (-)

Sehingga HPnya: {0° ≤ x < 30° atau 90° < x < 150° atau 270° < x ≤ 360°}

Sekian informasi mengenai persamaan dan pertidaksamaan trigonometri,