Percepatan Lengkap Contoh Soal Dan Pembahasannya
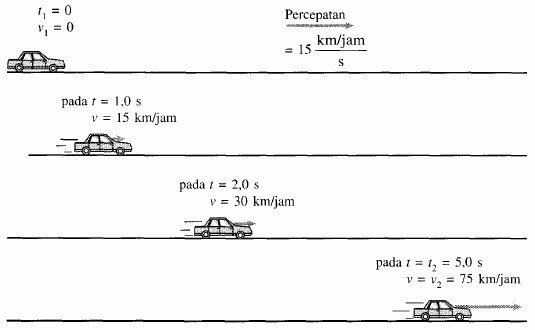
Contoh Soal Percepatan
Agar lebih jelas dalam menggunakan rumus percepatan tersebut, berikut ini akan diberikan contoh soal beserta jawabannya yang perlu anda ketahui.
1). Sebuah sepeda melaju dengan kecepatan 2m/s menjadi 6m/s selama 10 detik. Hitunglah percepatan yang dilakukan oleh motor tersebut !
Jawab :
v0 = 2m/s
vt= 6m/s
t = 6 sekon
= 6 – 2/10 = 4/10 = 0,4 m/s2
Jadi percepatan sepeda tersebut setelah 10 detik adalah 0, 4 m/s2
2). Sebuah mobil balap melaju dengan kecepatan awal 18,5 m/s kemudian kecepatannya bertambah secara konstan menjadi 46,1 m/s dalam kurun waktu 2,47 sekon. Hitunglah percepatan rata-rata mobil balap tersebut !
Jawab :
a= = vt – v0 / tt – t0
a = (46,1- 18,5) / 2,47 = 11,17 m/s2
Jadi percepatan rata-rata yang dialami oleh mobil balap tersebut adalah 11,17 m/s2.
Baca Juga :
Katrol Bergerak: Persamaan Tegangan Tali dan Percepatan
Hubungan antara Jarak, Waktu dan Kecepatan
Cara mengukur jarak tempuh, waktu tempuh, dan kecepatan rata-rata kendaraan
3). Sebuah mobil balap bergerak dalam lintasan lurus dan dinyatakan dalam persamaan v(t) = 10 – 8t + 6t2, dengan t dalam sekon dan v dalam m/s. Tentukan percepatan mobil balap tersebut pada saat t = 3 s!
Penyelesaian
Persamaan kedudukan v(t) = 10 – 8t + 6t2
Untuk t = 3 →v(3) = 10 – 8(3) + 6(3)2 = 40 m/s
Ambil 3 selang waktu (∆t) yang berbeda, misalkan ∆t1 = 0,1 s; ∆t2 = 0,01 s; ∆t3 = 0,001 s
Untuk ∆t = 0,1 s
t2 = t1 + ∆t
t2 = 3 + 0,1 = 3,1 s
v(3,1) = 10 – 8(3,1) + 6(3,1)2 = 42,86 m/s
a rata-rata = (v2– v1)/ (t2– t1)
a rata-rata = (42,86 – 40)/ (3,1 – 3)
a rata-rata = 28,6 m/s2
Untuk ∆t = 0,01 s
t2 = t1 + ∆t
t2 = 3 + 0,01 = 3,01 s
v(3,01) = 10 – 8(3,01) + 6(3,01)2 = 40,2806 m/s
a rata-rata = (v2– v1)/ (t2– t1)
a rata-rata = (40,2806 – 40)/ (3,01 – 3)
a rata-rata = 28,06 m/s2
Untuk ∆t = 0,001 s
t2 = t1 + ∆t
t2 = 3 + 0,001 = 3,001 s
v(3,001) = 10 – 8(3,001) + 6(3,001)2 = 40,028006 m/s
a rata-rata = (v2– v1)/ (t2– t1)
a rata-rata = (40,028006 – 40)/ (3,001 – 3)
a rata-rata = 28,006 m/s2
kemudian selang waktu dan percepatan rata-rata dimasukkan dalam tabel berikut ini:
| ∆t (s) | a (m/s2) |
| 0,1 | 28,6 |
| 0,01 | 28,06 |
| 0,001 | 28,006 |
Berdasarkan tabel di atas, nampak bahwa untuk nilai ∆t yang makin kecil (mendekati nol), percepatan rata-rata makin mendekati nilai 28 m/s2. Oleh karena itu, dapat disimpulkan bahwa percepatan sesaat pada saat t = 3 s adalah 28 m/s2.
4). Pak Nanda mengendarai sepeda dengan kecepatan 7,2 km/jam. Pada suatu tanjakan, siswa tersebut mengurangi kecepatannya sebesar 0,5 m/s2 selama 2 sekon. Berapakah kecepatan akhir siswa tersebut?
Penyelesaian
v1 = 7,2 km/jam
v1 = 7,2 (1.000/3.600) m/s
v1 = 2 m/s
a = −0,5 m/s2 (tanda negatif menunjukkan perlambatan)
t = 2 s
Ditanya = v2
Dari persamaan percepatan berikut:
a = (v2– v1)/t
Kita mendapatkan persamaan:
v2 = v1 +at
v2 = 2 + (−0,5 × 2)
v2 = 1 m/s
v2 = 3,6 km/jam
jadi, kecepatan akhirnya adalah 3,6 km/jam.
Artikel Terkait
- asd
- asd
- Sinonim akulturasi adalah kontak kabudayaan #sinonim #bahasa #akulturaasi #bahasaindonesia #antonim
- Pada Suatu Pertemuan, Hadir 10 Orang yang Saling Berjabat Tangan. Banyaknya Jabat Tangan yang Terjadi Adalah... Jawaban dan Pembahasan
- Suku Kelima Suatu Barisan Aritmatika Adalah 22, Sedangkan Kesembilan Adalah 42. Suku Kelima Belas Sama Dengan... Jawaban dan Pembahasan
- Mata Uang yang Sering Digunakan Sebagai Alat Pembayaran dan Kesatuan Hitung Dalam Transaksi Ekonomi dan Keuangan Internasional Disebut...
- Kingdom yang Tidak Memiliki Dinding Sel... Jawaban dan Pembahasan
- Organel Sel yang Berperan Untuk Mendetoksifikasi Racun Adalah... Jawaban dan Pembahasan
- Diketahui Harga 4 kg Jeruk, 1 kg Semangka, dan 2 kg Apel Adalah Rp 54.000,00. Harga 1 kg Jeruk, 2 kg Semangka, dan 2 kg Apel Adalah Rp 43.000,00. Sedangkan Harga 3 kg Jeruk, 1 kg Semangka, dan 1 kg Apel Adalah Rp 37.500,00. Berapakah Harga 1 kg Semangka?
- Nilai Rataan Hitung dari Data 4 10 7 x 10 6 11 Adalah 8 Nilai x Adalah ...