Metode Pembagian Suku Banyak / Polinomial

Materi kali ini mengenai polinomial atau sering disebut dengan suku banyak. Mengenai apa itu suku banyak dan bagaiman bentuknya, mari kita simak pada penjelasan dibawah ini.

Bentuk Umum

a_n xⁿ + a_{n – 1} x^{n – 1} + a_{n – 2} x^{n – 2} + … + … a₂x² + a₁x + a₀

keterangan :

n = derajat suku banyak

a₀ = konstanta

a_n, a_{n – 1}, a_{n – 2}, … = koefisien dari xⁿ, x^{n – 1}, x^{n – 2}, …

Pangkat merupakan bilangan cacah .

Pembagian Suku Banyak

Bentuk Umum

F(x) = P(x).H(x) + S(x)

dimana :

F(x) = suku banyak

P(x) = pembagi

H(x) = hasil bagi

S(x) = sisa

Teorema Sisa

Jika suatu suku banyak F(x) dibagi oleh (x – k) maka sisanya adalah F(k)

Jika pembagi berderajat n maka sisanya berderajat n – 1

Jika suku banyak berderajat m dan pembagi berderajat n, maka hasil baginya berderajat m – n

Metode Pembagian Suku Banyak

contoh :

F(x) = 2x³ – 3x² + x + 5 dibagi dengan P(x) = 2x² – x – 1

1. Pembagian Biasa

Sehingga hasil baginya: H(X) = x – 1, sisanya S(x) = x + 4

2. Cara Horner/skema

cara ini dapat  digunakan untuk pembagi berderajat 1 atau pembagi yang dapat difaktorkan menjadi pembagi-pembagi berderajat 1

Cara:

• Tulis koefisiennya saja → harus runtut dari koefisien xⁿ, x^{n – 1}, … hingga konstanta (jika ada variabel yang tidak ada, maka koefisiennya ditulis 0)

Contoh: untuk 4x³ – 1, koefisien-koefisiennya adalah 4, 0, 0, dan -1 (untuk x³, x², x, dan konstanta)

• Jika koefisien derajat tertinggi P(x) ≠ 1, maka hasil baginya harus dibagi dengan koefisien derajat tertinggi P(x)
• Jika pembagi dapat difaktorkan, maka:

Jika pembagi dapat difaktorkan menjadi P₁ dan P₂, maka S(x) = P₁.S₂ + S₁

Jika pembagi dapat difaktorkan menjadi P₁, P₂, P₃, maka S(x) = P₁.P₂.S₃ + P₁.S₂ + S₁

Jika pembagi dapat difaktorkan menjadi P₁, P₂, P₃, P₄, maka S(x) = P₁.P₂.P₃.S₄ + P₁.P₂.S₃ + P₁.S₂ + S₁

dan seterusnya

Untuk soal di atas,

P(x) = 2x² – x – 1 = (2x + 1)(x – 1)

P₁: 2x + 1 = 0 → x = –½

P₂: x – 1 = 0 → x = 1

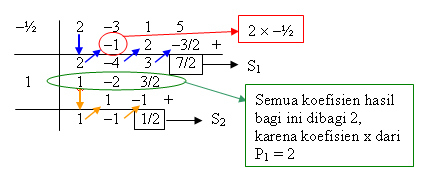
Cara Hornernya:

H(x) = 1.x – 1 = x – 1

S(x) = P₁.S₂ + S₁ = (2x + 1).1/2 + 7/2 = x + ½ + 7/2 = x + 4

Baca juga : Contoh Soal Pembagian Suku Banyak dan Metode Horner

3. Koefisien Tak Tentu

F(x) = P(x).H(x) + S(x)

Untuk soal di atas, karena F(x) berderajat 3 dan P(x) berderajat 2, maka

H(x) berderajat 3 – 2 = 1

S(x) berderajat 2 – 1 = 1

Jadi, misalkan H(x) = ax + b dan S(x) = cx + d

Maka:

2x³ – 3x² + x + 5 = (2x² – x – 1).(ax + b) + (cx + d)

Ruas kanan:

= 2ax³ + 2bx² – ax² – bx – ax – b + cx + d

= 2ax³ + (2b – a)x² + (–b – a + c)x + (–b + d)

Samakan koefisien ruas kiri dan ruas kanan:

x³ → 2 = 2a → a = 2/2 = 1

x² → –3 = 2b – a → 2b = –3 + a = –3 + 1 = –2 → b = –2/2 = –1

x → 1 = –b – a + c → c = 1 + b + a = 1 – 1 + 1 → c = 1

Konstanta → 5 = –b + d → d = 5 + b = 5 – 1 → d = 4

Jadi:

H(x) = ax + b = 1.x – 1 = x – 1

S(x) = cx + d = 1.x + 4 = x + 4

 

Teorema Faktor

Suatu suku banyak F(x) mempunyai faktor (x – k) jika F(k) = 0 (sisanya jika dibagi dengan (x – k) adalah 0)

Catatan: jika (x – k) adalah faktor dari F(x) maka k dikatakan sebagai akar dari F(x)

Tips

1. Untuk mencari akar suatu suku banyak dengan cara Horner, dapat dilakukan dengan mencoba-coba dengan angka dari faktor-faktor konstanta dibagi faktor-faktor koefisien pangkat tertinggi yang akan memberikan sisa = 0. Contohnya :untuk x³ – 2x² – x + 2 = 0, faktor-faktor konstantanya: ±1, ±2, faktor-faktor koefisien pangkat tertinggi: ±1. Sehingga, angka-angka yang perlu dicoba: ±1 dan ±2untuk 4x³ – 2x² – x + 2 = 0, faktor-faktor konstantanya: ±1, ±2, faktor-faktor koefisien pangkat tertinggi: ±1, ±2, ±4. Sehingga, angka-angka yang perlu dicoba: ±1, ±2, ±1/2, ±1/4
2. Jika jumlah koefisien suku banyak = 0, maka pasti salah satu akarnya adalah x = 1.
3. Jika jumlah koefisien suku di posisi genap = jumlah koefisien suku di posisi ganjil, maka pasti salah satu akarnya adalah x = –1

Perhatikan contoh berikut :

Tentukan penyelesaian dari x³ – 2x² – x + 2 = 0?

Jawab :

Faktor-faktor dari konstantanya, yaitu 2,  adalah ±1 dan ±2 dan faktor-faktor koefisien pangkat tertingginya, yaitu 1, adalah ±1, sehingga angka-angka yang perlu dicoba: ±1 dan ±2

Karena jumlah seluruh koefisien + konstantanya = 0 (1 – 2 – 1 + 2 = 0), maka, pasti x = 1 adalah salah satu faktornya, jadi:

Jadi x³ – 2x² – x + 2 = (x – 1)(x² – x – 2)

= (x – 1)(x – 2)(x + 1)

x = 1   x = 2   x = –1

Jadi himpunan penyelesaiannya: {–1, 1, 2}

Sifat Akar-Akar Suku Banyak

Pada persamaan berderajat 3:

ax³ + bx² + cx + d = 0 akan mempunyai akar-akar x₁, x₂, x₃

dengan sifat-sifat:

• Jumlah 1 akar: x₁ + x₂ + x₃ = – b/a
• Jumlah 2 akar: x₁.x₂ + x₁.x₃ + x₂.x₃ = c/a
• Hasil kali 3 akar: x₁.x₂.x₃ = – d/a

Pada persamaan berderajat 4:

ax⁴ + bx³ + cx² + dx + e = 0 akan mempunyai akar-akar x₁, x₂, x₃, x₄

dengan sifat-sifat:

• Jumlah 1 akar: x₁ + x₂ + x₃ + x₄ = – b/a
• Jumlah 2 akar: x₁.x₂ + x₁.x₃ + x₁.x₄ + x₂.x₃ + x₂.x₄ + x₃.x₄ = c/a
• Jumlah 3 akar: x₁.x₂.x₃ + x₁.x₂.x₄ + x₂.x₃.x₄ = – d/a
• Hasil kali 4 akar: x₁.x₂.x₃.x₄ = e/a

Dari kedua persamaan tersebut, kita dapat menurunkan rumus yang sama untuk persamaan berderajat 5 dan seterusnya

(amati pola:  –b/a, c/a, –d/a , e/a, …)

 

Pembagian Istimewa

Baca juga : Contoh Soal Pembagian Suku Banyak dan Metode Horner