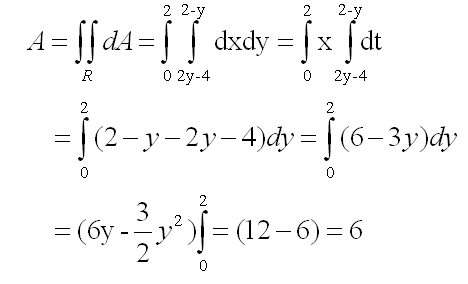
Integral yang akan kita bahas kali ini yaitu integral lipat dua, sebuah integral lanjutan yang tak boleh kita lupakan. Untuk menambah kecintaan kepada matematika tentunya kita harus memahami berbagai konsep matematika termasuk integral yang pada kesempatan kali ini dibahas integral lipat dua.

Integral lipat dua ini biasanya digunakan untuk menghitung luas. Perhatikan penjelasan dibawah ini.

Integral untuk fungsi satu variabel kita membentuk suatu partisi dari interval [a,b] menjadi interval-interval yang panjangnya Δx_k ,  k = 1, 2, 3, 4, ….n.

Dengan cara yang sama, kita definisikan untuk dua variabel. Misalkan terdapat fungsi z=f(x,y) untuk daerah tertutup R dibidang xoy. Selanjutnya daerah ini dibagi atas n buah sub daerah yang masing-masing memiliki luas A1, A2, A3,…,An. Dalam setiap sub daerah pilihlah suatu titik P_k(x_k, y_k)  dan bentuklah

Jika jumlah sub daerah makin besar hingga menuju tak hingga maka integral lipat dari daerah R didefinisikan

Untuk menghitung integral lipat dua kita dapat menggunakan integral berulang yang ditulis dalam bentuk

Baik kita menggunakan cara a atau cara b jika integralnya memberikan hasil maka hasilnya akan sama.

Integral Lipat Dua Dengan Batas Persegi Panjang

Bentuk umum

Integral Lipat Dua Dengan Batas Bukan Persegi Panjang

Bentuk Umum

Aplikasi Integral Lipat Dua

Integral lipat dua dengan bentuk umum ∫∫f(x,y) dA biasanya digunakan untuk menghitung luas. Luas dari suatu bidang dapat dipandang dengan sustu integral lipat dua jika f(x,y)=1 sehingga integral lipat dua menjadi

contoh soal :

Hitung luas daerah yang dibatasi oleh x + y = 2 dan 2y = x + y

Jawab :

Sekian ulasan tentang Integral lipat dua, semoga sekarang anda telah memahami materi tentang integral lipat dua ini. Sehingga jika anda menemukan soal mengenai integral lipat dua sampai aplikasinya yang biasa digunakan untuk menghitung luas anda sudah tidak kesulitan.

Dengan semakin kita mengerti materi dalam matematika semakin kita cinta pada matematika, Selamat Belajar dan Semoga Berhasil