Materi Fungsi Komposisi Serta Cara Cepat Menyelesaikan Soal-soalnya

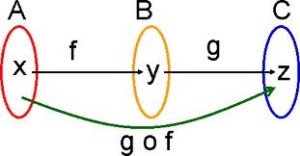
Misalkan kita memiliki fungsi f(x) = 2x + 3 dengan domainnya adalah bilangan real, dan g(x) = √(x – 1) dengan domain x ≥ 1 untuk x bilangan real. Fungsi komposisi g ○ f dapat digambarkan sebagai berikut.

Mula-mula x merupakan anggota domain f yang selanjutnya dipetakan oleh f ke bayangan x, yaitu f(x). Dari f(x) dipetakan kembali oleh g ke g(f(x)). Dengan demikian fungsi komposisi g ○ f adalah pemetaan x anggota domain f oleh fungsi f, selanjutnya bayangannya dipetakan kembali oleh g. Uraian tersebut memperjelas definisi dari fungsi komposisi berikut.

Diketahui f dan g dua fungsi sembarang, maka fungsi komposisi f dan g ditulis g ○ f didefinisikan sebagai (g ○ f)(x) = g(f(x)) untuk setiap x anggota domain f.

Syarat yang harus dipenuhi agar fungsi f dan fungsi g dapat dikomposisikan menjadi fungsi komposisi g ○ f adalah irisan antara daerah hasil fungsi f dan daerah asal fungsi g bukan himpunan kosong.

Perhatikan contoh berikut :

1. Jika f(x) = 2x + 3 dan (f o g) = 2x² + 6x – 7, maka g(x) = …

2. Fungsi g: R → R ditentukan oleh g(x) = x² – 3x + 1 dan f: R → R sehingga (f o g)(x) = 2x² – 6x – 1

maka f(x) = ….

Penyelesaian :

(f o g)(x)            = 2x² – 6x – 1

 f (g(x))             = 2x² – 6x – 1

 f ( x² – 3x + 1)  = 2x² – 6x – 1

                           = 2 ( x² – 3x + 1 ) – 3

Jadi       f (x)      = 2x – 3

 

3. Jika f(x) = x² + 3x dan g(x) = x – 12, maka nilai (f o g)(8) adalah ….

Penyelesaian :

 g(8) = 8 – 12 = – 4

jadi (f o g) (8) = f(g(8)) = f(-4) = (-4)² + 3(-4) = 16 – 12 = 4

 

4. Diketahui (f o g)(x) = x² + 3x + 4 dan g(x) = 4x – 5. Nilai dari f(3) adalah ….

Penyelesaian :

 

(f o g)(x)     = x² + 3x + 4

f (g(x))        =  x² + 3x + 4

 

Untuk    g(x)    = 3              maka

           4x – 5   = 3

                   4x = 8

                    x = 2

 

Karena  f (g(x))  =  x² + 3x + 4   dan  untuk g(x) = 3 didapat x = 2

 

Sehingga :

 

f (3) =  2² + 3 . 2 + 4   =   4 + 6 + 4   =   14

 

 

INVERS FUNGSI KOMPOSISI

Misalnya diketahui  fungsi f : A  B dan g : B  C. Jika h adalah fungsi komposisi dari f atau g .

 

 

 

dengan

 

 

 maka invers  fungsi h adalah

  

 

dengan

  

 

jadi jika

  

 

maka

 .

 

Sedikit penjelasan mengenai fungsi komposisi ini mudah-mudahan dapat membantu sobat semua dalam proses belajar matematika lebih dalam. Janganlah cepat menyerah dalam mempelajari sesuatu termasuk matematika, karena semakin kita tahu maka akan semakin menyenangkan dijalani, karena matematika itu menyenangkan.