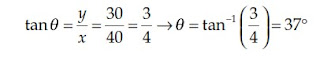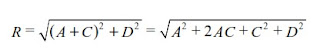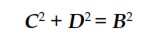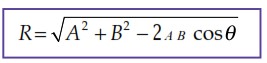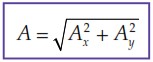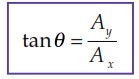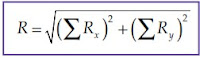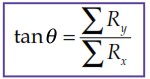Materi Besaran dan Resultan Vektor dalam Fisika Lengkap

Besaran vektor adalah besaran yang mempunyai nilai (besar) dan arah. Contoh besaran vektor, antara lain, perpindahan, kecepatan, percepatan, momentum, dan gaya. Untuk menyatakan besaran vektor, harus menggunakan nilai (angka) dan disebutkan arahnya. Misalnya, Nisa berlari ke utara dengan kecepatan 5 km/jam dan Robert menggeser almari sejauh 3 meter ke barat.

Untuk lebih jelasnya kalian bisa simak video di bawah ini yah otakers !

Sumber: https://www.youtube.com/watch?v=a2kHJ886XfA

A. Penulisan dan Penggambaran Vektor

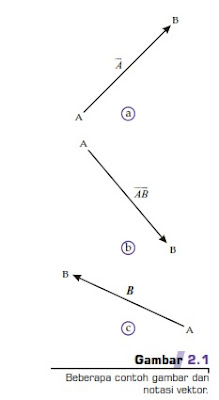
Sebuah vektor digambarkan oleh sebuah anak panah. Panjang anak panah mewakili besar atau nilai vektor, sedangkan arah anak panah mewakili arah vektor. Notasi atau simbol sebuah vektor dapat menggunakan satu atau dua huruf dengan tanda panah di atasnya, misalnya A atau AB . Akan tetapi, dalam buku ini, vektor digambarkan oleh sebuah huruf yang dicetak tebal dan miring, misalnya A atau B. Gambar 2.1 menunjukkan gambar beberapa vektor dengan notasinya. Titik A disebut titik pangkal vektor dan titik B disebut ujung vektor.

Besar sebuah vektor dapat ditulis dengan beberapa cara, di antaranya dengan memberi tanda mutlak (||) atau dicetak miring tanpa ditebalkan. Sebagai contoh, besar vektor A ditulis |A|atau A dan besar vektor B ditulis |B|atau B.

Arah sebuah vektor dinyatakan oleh sudut tertentu terhadap arah acuan tertentu. Umumnya, sudut yang menyatakan arah sebuah vektor dinyatakan terhadap sumbu-x positif. Gambar 2.2 memperlihatkan tiga buah vektor A, B, dan C dengan arah masing-masing membentuk sudut 45°, 90°, dan 225° terhadap sumbu-x positif.

B. Penjumlahan Vektor Menggunakan Metode Grafis dan Analitis

Pernahkah Anda membayangkan jika Anda berenang di sungai searah dengan aliran sungai, kemudian Anda tiba-tiba berbalik arah 90° dari arah pergerakan semula? Apakah posisi terakhir Anda tepat sesuai keinginan

Anda? Tentu tidak, arah akhir posisi Anda tidak akan membentuk sudut 90° dari posisi semula karena terdapat hambatan arus sungai yang membuat arah gerak Anda tidak tepat atau menyimpang. Anda dapat menentukan posisi akhir Anda dengan cara menjumlahkan vektor gerak Anda, baik perpindahannya maupun kecepatannya. Apakah Anda mengetahui cara menjumlahkan dua buah vektor?

Penjumlahan vektor tidak sama dengan penjumlahan skalar. Hal ini karena vektor selain memiliki nilai, juga memiliki arah. Vektor yang diperoleh dari hasil penjumlahan beberapa vektor disebut vektor resultan. Berikut ini akan dibahas metode-metode untuk menentukan vektor resultan.

1. Resultan Dua Vektor Sejajar

Misalnya, Anda bepergian mengelilingi kota Palu dengan mengendarai sepeda motor. Dua jam pertama, Anda bergerak lurus ke timur dan menempuh jarak sejauh 50 km. Setelah istirahat secukupnya, Anda kembali melanjutkan perjalanan lurus ke timur sejauh 30 km lagi. Di lihat dari posisi asal, Anda telah berpindah sejauh sejauh 50 km + 30 km = 80 km ke timur. Dikatakan, resultan perpindahan Anda adalah 80 km ke timur. Secara grafis, perpindahan Anda seperti diperlihatkan pada Gambar 2.3.

Sedikit berbeda dengan kasus tersebut, misalnya setelah menempuh jarak lurus 50 km ke timur, Anda kembali lagi ke barat sejauh 30 km. Relatif terhadap titik asal, perpindahan Anda menjadi 50 km – 30 km = 20 km ke timur. Secara grafis, perpindahan Anda diperlihatkan pada Gambar 2.4.

Dari kedua contoh, seperti yang diperlihatkan pada Gambar 2.3 dan Gambar 2.4, menjumlahkan dua buah vektor sejajar mirip dengan menjumlahkan aljabar biasa. Secara matematis, resultan dua buah vektor sejajar, yakni, sebagai berikut. Jika vektor A dan B searah, besar vektor resultan R, adalah 

dengan arah vektor R sama dengan arah vektor A dan B. Sebaliknya, jika kedua vektor tersebut berlawanan, besar resultannya adalah

dengan arah vektor R sama dengan arah vektor yang terbesar.

2. Resultan Dua Vektor yang Saling Tegak Lurus

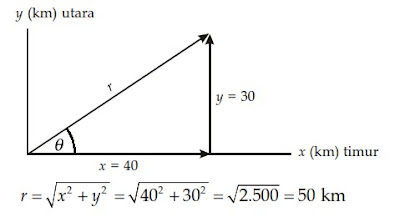
Misalnya, Anda memacu kendaraan Anda lurus ke timur sejauh 40 km dan kemudian berbelok tegak lurus menuju utara sejauh 30 km. Secara grafis, perpindahan Anda seperti diperlihatkan pada Gambar 2.5. Besar resultan perpindahannya, r,  diperoleh menggunakan Dalil Pythagoras, yakni sebagai berikut

dan arahnya

terhadap sumbu-x positif (atau 37° dari arah timur).

Dari contoh kasus tersebut, jika dua buah vektor, A dan B, yang salingtegak lurus akan menghasilkan vektor resultan, R, yang besarnya

terhadap arah vektor A dengan catatan vektor B searah sumbu-y dan vektor A searah sumbu-x.

3. Resultan Dua Vektor yang Mengapit Sudut

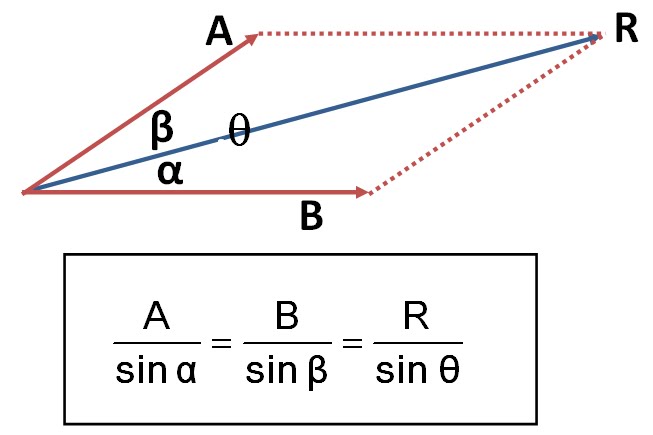
Sekarang tinjau dua buah vektor, A dan B, yang satu sama lain mengapit sudut seperti yang diperlihatkan pada Gambar 2.6 (a). Gambar vektor resultannya dapat diperoleh dengan cara menempatkan pangkal vektor B di ujung vektor A. Selanjutnya, tarik garis dari titik pangkal vektor A ke titik ujung vektor B dan buatkan panah tepat di ujung yang berimpit dengan ujung vektor B. Vektor inilah, R, resultan dari vektor A dan B. Hasilnya seperti diperlihatkan pada Gambar 2.6 (b).

Besar vektor resultan, R, dapat ditentukan secara analitis sebagai berikut. Perhatikan Gambar 2.7. Vektor C dan D diberikan sebagai alat bantu sehingga vektor A + C tegak lurus vektor D dan ketiganya membentuk resultan yang sama dengan resultan dari vektor A dan B, yakni R . Dengan menggunakan Dalil Pythagoras, besarnya vektor resultan R adalah

Selanjutnya, juga dengan menggunakan Dalil Pythagoras, dari gambar diperoleh

dan dari trigonometri,

Dengan memasukkan dua persamaan terakhir ke persamaan pertama, diperoleh besarnya vektor resultan R.

4. Selisih Dua Vektor yang Mengapit Sudut

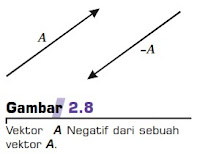
Vektor A dan vektor -A, memiliki besar yang sama, yakni |A| = |–A| = A, tetapi arahnya berlawanan seperti diperlihatkan pada Gambar 2.8. Selisih dari dua buah vektor, misalnya vektor A – B, secara grafis sama dengan jumlah antara vektor A dan vektor –B, seperti diperlihatkan pada Gambar 2.9. Secara matematis, vektor selisihnya ditulis R = A – B. 

Secara analitis, besar vektor selisihnya ditentukan dari Persamaan (2–5) dengan mengganti θ  dengan 180 – θ. Oleh karena, cos (180° – θ) = –cos θ sehingga diperoleh 

5. Melukis Resultan Beberapa Vektor dengan Metode Poligon

Jika terdapat tiga buah vektor, A, B, dan C, yang besar dan arahnyaberbeda seperti diperlihatkan pada Gambar 2.10 (a), resultannya dapat diperoleh dengan cara menggunakan metode poligon, yakni sebagai berikut.

• Hubungkan titik tangkap vektor B pada ujung vektor A dan titik pangkal vektor C pada ujung vektor B.

• Buat vektor resultan, R, dengan titik tangkap sama dengan titik pangkal vektor A dan ujung panahnya tepat di titik ujung vektor C. Hasilnya seperti diperlihatkan pada Gambar 2.10 (b).

Secara matematis, vektor resultan pada Gambar 2.10 ditulis sebagai berikut.

R = A + B + C

6. Vektor Nol

Vektor nol adalah vektor hasil penjumlahan beberapa buah vektor yang hasilnya nol. Sebagai contoh, lima buah vektor, A, B, C, D, dan E, menghasilkan resultan sama dengan nol maka secara matematis ditulis A + B + C + D + E = 0 Dengan menggunakan metode poligon, secara grafis vektor-vektor tersebut diperlihatkan seperti pada Gambar 2.11. Perhatikan bahwa ujung vektor terakhir (vektor E) bertemu kembali dengan titik pangkal vektor pertama (vektor A).

Baca Juga :

Apa itu Besaran Skalar dan Besaran Vektor ?

Vektor : Contoh Soal dan Pembahasannya

 C Menjumlahkan Vektor dengan Metode Uraian

Dalam beberapa kasus, seringkali Anda menjumlahkan beberapa vektor yang lebih dari dua buah. Secara grafis, metode yang digunakan adalah metode poligon, seperti yang telah disinggung sebelumnya. Akan tetapi, bagaimanakah cara menentukan besar dan arah vektor resultannya? Salah satu metode yang digunakan adalah metode uraian, seperti yang akan di bahas pada sub-subbab berikut ini.

1. Menguraikan Vektor Menjadi Vektor Komponennya

Sebuah vektor dapat diuraikan menjadi dua buah vektor yang saling tegak lurus. Vektor-vektor baru hasil uraian disebut vektor-vektor komponen. Ketika sebuah vektor telah diuraikan menjadi vektor-vektor komponennya, vektor tersebut dianggap tidak ada karena telah diwakili oleh vektor-vektor komponennya. Sebagai contoh, ketika Anda menguraikan sekarung beras 50 kg menjadi dua karung dengan masing-masing 20 kg dan 30 kg, apakah karung yang berisi 50 kg tetap ada?

Gambar 2.12 memperlihatkan sebuah vektor A yang diuraikan menjadi dua buah vektor komponen, masing-masing berada pada sumbu-x dan sumbu-y. Ax adalah komponen vektor A pada sumbu-x dan Ay adalah komponen vektor A pada sumbu-y. Dengan mengingat definisi sin θ  dan cos θ dari trigonometri, besar setiap komponen vektor A dapat ditulis sebagai berikut.

Sementara itu, dengan menggunakan Dalil Pythagoras diperoleh hubungan

Selanjutnya, hubungan antara Ax dan Ay diberikan oleh

2. Menjumlahkan Vektor Melalui Vektor-Vektor Komponennya

Menjumlahkan sejumlah vektor dapat dilakukan dengan menguraikan setiap vektor menjadi komponen-komponennya ke sumbu-x dan sumbu-y pada koordinat kartesius. Metode seperti ini disebut metode uraian.

Berikut adalah tahapan-tahapan untuk mencari besar dan arah vektor resultan dengan metode uraian.

• Buat koordinat kartesius x-y.

• Letakkan titik tangkap semua vektor pada titik asal (0,0). Hati-hati, arah vektor tidak boleh berubah.

• Uraikan setiap vektor, yang tidak berimpit dengan sumbu-x atau sumbu-y,menjadi komponen-komponennya pada sumbu-x dan sumbu-y.

• Tentukanlah resultan vektor-vektor komponen pada setiap sumbu,misalnya
  ∑Rx= resultan vektor-vektor komponen pada sumbu-x.
  ∑Ry =resultan vektor-vektor komponen pada sumbu-y.

• Besar vektor resultannya

dan arahnya terhadap sumbu-x positif

Simak video di bawah ini yah !

Sumber: https://www.youtube.com/watch?v=GyWxS4MOJXU