Home » Kongkow » Materi » Kesebangunan dan Kekongruenan Matematika

Kesebangunan dan Kekongruenan Matematika

- Rabu, 25 September 2019 | 13:00 WIB

pada halaman ini kita akan mengupas tentang contoh soal kesebangunan dan kekongruenan. Seperti kisi-kisi yang telah dikeluarkan BSNP, materi kesebangunan dan kekongruenan akan kembali muncul di ujian nasional tahun 2018. Kisi-kisi untuk kesebangunan dan kekongruenan diberikan dalam 3 (tiga) level kognitif, yaitu pengetahuan dan pemahaman, aplikasi, dan penalaran. Halaman ini akan membahas kisi-kisi UN 2018 dengan materi kesebangunan dan kekongruenan untuk level penalaran. Simak kumpulan soal UN dengan materi kesebangunan dan kekongruenan pada pembahasan di bawah.

Contoh 1: Soal UN MATEMATIKA SMP 2016
Perhatikan gambar berikut!

Jika CF : FB = 2 : 3 dan CD = 12 cm, maka panjang EF adalah ….
A. 6 cm
B. 9 cm
C. 12 cm
D. 18 cm

Pembahasan:
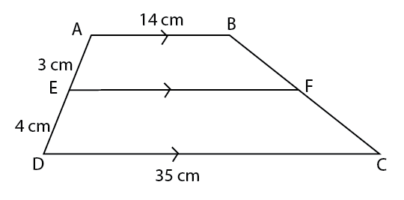
Berdasarkan keterangan pada soal, kita dapat mengetahui ukuran masing-masing sisi, seperti terlihat pada gambar berikut.
kesebangunan dan kekongruenan

Untuk menghitung EF, gunakan rumus di bawah.

$EF =\frac{CD \times FB + AB \times CF}{FB + CF}$

Sehingga,

$EF =\frac{12 \times 3x + 27 \times 2x}{3x + 2x}$

$EF =\frac{36x + 54x}{5x}$

$EF =\frac{90x}{5x}\;=\;18\;cm$

Jawaban: D

Contoh 2: SOAL UN MATEMATIKA SMP 2016
“Lebar Sungai”
Andi ingin mengetahui lebar sungai. Di seberang sungai terdapat sebuah pohon. Untuk itu dia menancapkan tongkat sehingga berada pada posisi A, B, C, dan D dengan ukuran seperti pada gambar.
Kesebangunan dan Kekongruenan
Andi ingin mengukur lebar sungai dari tongkat D sampai pohon. Berapa lebar sungai tersebut?
A. 11 m
B. 12 m
C. 15 m
D. 16 m

Pembahasan:
Perhatikan sketsa berikut!

Lebar sungai dapat dihitung dengan memanfaatkan kesebangunan segitiga.
Lebar sungai = DP

$\frac{DP}{AP} = \frac{DC}{AB}$

$\frac{DP}{4 + DP} = \frac{6}{8}$

$8DP = 6 \times (4 + DP)$

$\[ 8DP = 24 <a href=$ + 6DP) \]" src="https://idschool.net/wp-content/ql-cache/quicklatex.com-2a96849d13dfcaf2cc7622eaa4da0d1e_l3.svg" style="height:16px; width:119px" title="Rendered by QuickLaTeX.com" />

$8DP - 6DP = 24$

$2DP = 24$

$DP = \frac{24}{2} = 12 \; m$

Jadi, lebar sungai = DP = 12 m.
Jawaban: B

Contoh 3: Soal UN Matematika SMP/MTS Tahun 2013
Perhatikan gambar!
Contoh soal un matematika SMP/MTs
Panjang EF adalah ….
A. 20 cm
B. 21 cm
C. 23 cm
D. 26 cm

Pembahasan:
Rumus singkat untuk mencari panjang EF adalah sebagai berikut.

$EF = \frac{AB \times DE + DC \times AE}{DE + AE}$

$EF = \frac{14 \times 4 + 35 \times 3}{4 + 3}$

$EF = \frac{56 + 105}{7}$

$EF = \frac{161}{7} = 23 \; cm$
Jawaban: C

Contoh 4: Soal UN Matematika SMP/MTS Tahun 2011
Perhatikan gambar berikut!
soal un matematika kesebangunan
Segitiga ABC adalah segitiga siku-siku samakaki. Jika AB = 10 cm dan CD garis bagi sudut C, panjang BD adalah ….

$\textrm{A.} \; \; \; 5 \; cm$

$\textrm{B.} \; \; \; \left(10 \sqrt{2} − 10 \right) \; cm$

$\textrm{C.} \; \; \; \left(10 − 5 \sqrt{2} \right) \; cm$

$\textrm{D.} \; \; \; \left( 5 \sqrt{2} − 5 \right) \; cm$
Pembahasan:
Perhatikan gambar di bawah!
kesebangunan dan kekongruenan
Berdasarkan gambar, diperoleh informasi bahwa
AB = BC = CE = 10 cm
BD = DE = AE

Mencari nilai AC:
Perhatikan $\Delta ABC$
Besar sudut BCA adalah $45^{o}$ (segitiga siku-siku samakaki), sehingga

$AB : AC = 1 : \sqrt{2}$

$\frac{AB}{AC} = \frac{1}{\sqrt{2}}$

$\frac{10}{AC} = \frac{1}{\sqrt{2}}$

$AC =10 \sqrt{2}$
Mencari panjang BD:

$BD = AE$

$BD = AC - CE$

$BD = \left( 10 \sqrt{2} - 10 \right) \; cm$

Jawaban: B

Contoh 5: Soal UN Matematika SMP/MTS Tahun 2010
Perhatikan gambar!
kesebangunan dan kekongruenan
P dan Q adalah titik tengah diagonal BD dan AC. Panjang PQ adalah .…
A. 5 cm
B. 4 cm
C. 3 cm
D. 2 cm

Pembahasan:
Rumus cepat untuk mendapatkan panjang PQ adalah

$PQ = \frac{1}{2} \left(DC - AB \right)$

$PQ = \frac{1}{2} \left(12 - 6 \right)$

$PQ = \frac{1}{2} \times 6$

$PQ = 3 \; cm$

Jawaban: C

Contoh 6: Soal UN Matematika SMP/MTS Tahun 2007
Segitiga ABC siku-siku di B kongruen dengan segitiga PQR siku-siku di P. Jika panjang BC = 8 cm dan QR = 10 cm, maka luas segitiga PQR adalah ….
A. 24 $cm^{2}$
B. 40 $cm^{2}$
C. 48 $cm^{2}$
D. 80 $cm^{2}$

Pembahasan:
Perhatikan gambar di bawah!
kekongruenan segitiga
Segitiga ABC dan PQR kongruen, sehingga panjang BC = PQ = 8 cm. Panjang RP dapat diperoleh menggunakan rumus pythagoras.