Home » Kongkow » Materi » Katrol Bergerak: Persamaan Tegangan Tali dan Percepatan

Katrol Bergerak: Persamaan Tegangan Tali dan Percepatan

- Senin, 05 Agustus 2019 | 19:00 WIB

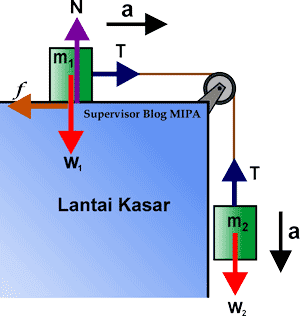
Katrol merupakan salah satu pesawat sederhana yang cukup mudah dijumpai. Misalnya pada timba sumur, katrol dimanfaatkan untuk mengambil air dari dasar sumur ke permukaan. Contoh katrol yang dijumpai pada timba air merupakan jenis katrol tetap. Ada sebuah jenis katrol lain, yaitu katrol bebas atau yang sering juga disebut dengan katrol bergerak. Dikatakan sebagai katrol bergerak karena posisinya berubah-ubah (tidak tetap). Contoh pemanfaatan katrol bergerak terdapat pada alat pengangkat petikemas.

Katrol Bebas

Menurut wikipedia, petikemas diartikan sebagai peti atau kotak yang memenuhi persyaratan teknis sesuai dengan International Organization for Standardization (ISO) sebagai alat atau perangkat pengangkutan barang. Di dalam isi petikemas memuat barang-barang yang akan diangkut untuk distribusi bahan berbagai keperluan di berbagai wilayah. Untuk mengangkat petikemas, biasanya digunakan alat berat yang memanfaatkan katrol bergerak di dalamnya.

Alasan penggunaan katrol bergerak dikarenakan katrol ini memiliki keuntungan mekanis sebesar dua. Artinya, seseorang hanya memerlukan setengah dari berat benda untuk mengangkat benda tersebut menggunakan katrol bergerak.

Untuk mengetahui prinsip kerja dari katrol bergerak, akan dijelaskan lebih lengkap melalui uraian di bawah. Ulasan meliputi persamaan gerak benda pada katrol bergerak, berupa persamaan gaya tegangan tali dan rumus percepatan gerak benda pada katrol bergerak.

Simak uraian penjelasannya di bawah.

Persamaan Gaya Tegangan Tali pada Katrol Bergerak

Persamaan gerak benda pada katrol bergerak tidak lepas dari Hukum Newton. Persamaan yang diperoleh merupakan jumlahan gaya yang bekerja pada katrol tersebut. Kita akan melihat persamaan dari sebuah contoh sistem katrol.

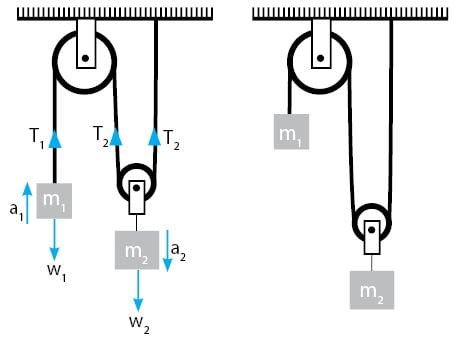
Diberikan sebuah sistem katrol, terdiri atas sebuah katrol tetap dan sebuah katrol bergerak. Gambarnya terlihat seperti berikut.

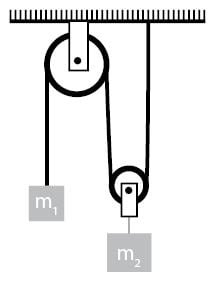
Katrol Bergerak

Perhatikan gambar di atas!

Jika massa benda pertama lebih besar maka benda pertama akan turun dan benda ke dua akan naik. Sebaliknya, jika massa benda ke dua lebih besar maka benda ke dua akan turun dan benda pertama akan naik. Terdapat dua kondisi di sini. Untuk itu, kita juga akan membahas persamaan pada katrol bergerak sesuai dengan kondisi yang terjadi.

Kondisi Pertama: Massa balok pertama lebih besar, sehingga benda pertama turun dan benda ke dua akan naik. Detail gaya pada sistem katrol menjadi seperti terlihat pada gambar di bawah.

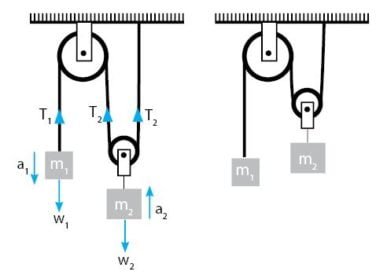
Gaya Tegangan Tali pada Katrol Bebas

Persamaan yang bisa diperoleh adalah sebagai berikut.

Resultan Gaya pada Balok 1:

Berdasarkan Hukum II Newton, resultan gaya dinyatakan melalui persamaan di bawah.

$\Sigma F_{1} = m_{1} \times a_{1}$

Balok 1 bergerak ke bawah, maka gaya yang arahnya ke bawah betanda positif sedangkan gaya yang arahnya ke atas tandanya negatif. Sehingga diperoleh persamaan di bawah.

$\[ w_{1} - T_{1} <a href=$ = m_{1} \times a_{1} \]" src="https://idschool.net/wp-content/ql-cache/quicklatex.com-cbb53711c6240fa7f748ed84efed9707_l3.svg" style="height:14px; width:119px" title="Rendered by QuickLaTeX.com" />

$m_{1} \times g - T_{1} = m_{1} \times a_{1}$

$T_{1} = m_{1} \times g - m_{1} \times a_{1}$

Resultan Gaya pada Balok 2:

Balok 2 bergerak ke atas, maka gaya yang arahnya ke atas bertanda positif sedangkan gaya yang arahnya ke bawah bertanda negatif.

$\Sigma F_{2} = m_{2} \times a_{2}$

$T_{2} + T_{2} - w_{2} = m_{2} \times a_{2}$

$2 \cdot T_{2} - w_{2} = m_{2} \times a_{2}$

$2 \cdot T_{2} = w_{2} + m_{2} \times a_{2}$

$\[ 2 \cdot T_{2} <a href=$ = m_{2} \times g + m_{2} \times a_{2} \]" src="https://idschool.net/wp-content/ql-cache/quicklatex.com-d89da4239fd5d75c01baea5b152d99df_l3.svg" style="height:14px; width:165px" title="Rendered by QuickLaTeX.com" />

$\[ T_{2} <a href=$ = \frac{m_{2} \times g + m_{2} \times a_{2}}{2} \]" src="https://idschool.net/wp-content/ql-cache/quicklatex.com-bdcf9a06d2bb837138f9348c3cf22d8b_l3.svg" style="height:29px; width:148px" title="Rendered by QuickLaTeX.com" />

Diperoleh dua persamaan tegangan tali pada sistem katrol seperti di bawah.

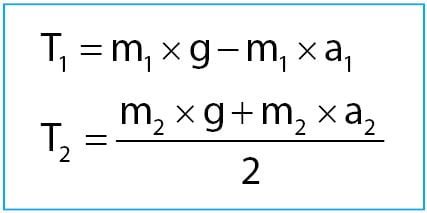
Persamaan Tegangan Tali pada Katrol Bebas

Untuk kondisi yang ke dua tidak akan jauh beda dengan cara di atas. Perbedaan hanya terletak pada tanda positif dan negatif yang digunakan untuk menentukan arah gerak benda.

Simak persamaan-persamaan yang berlaku untuk kondisi ke dua pada pembahasan berikut.

Percepatan Lengkap Contoh Soal Dan Pembahasannya

Menentukan Kecepatan Minimal Benda di Titik Terendah agar dapat Bergerak Melingkar Penuh

Kondisi Ke Dua: Massa balok ke dua lebih besar, sehingga benda ke dua turun dan benda pertama akan naik. Detail gaya pada sistem katrol menjadi seperti terlihat pada gambar di bawah.

Gaya Tegangan Tali pada Katrol Bebas 1

Persamaan yang bisa diperoleh adalah sebagai berikut.

Resultan Gaya pada Balok 1:

Berdasarkan Hukum II Newton, resultan gaya dinyatakan melalui persamaan di bawah.

$\Sigma F_{1} = m_{1} \times a_{1}$

Balok 1 bergerak ke atas, maka gaya yang arahnya ke atas berharga positif sedangkan gaya yang arahnya ke bawah berharga negatif. Sehingga diperoleh persamaan di bawah.

$T_{1} - w_{1} = m_{1} \times a_{1}$

$T_{1} - m_{1} \times g = m_{1} \times a_{1}$

$T_{1} = m_{1} \times a_{1} + m_{1} \times g$

Resultan Gaya pada Balok 2:

Balok 2 bergerak ke bawah, maka gaya yang arahnya ke bawah bertanda positif sedangkan gaya yang arahnya ke atas bertanda negatif.

$\Sigma F_{2} = m_{2} \times a_{2}$

$w_{2} - T_{2} - T_{2} = m_{2} \times a_{2}$

$w_{2} - 2 \cdot T_{2} = m_{2} \times a_{2}$

$m_{2} \times g - 2 \cdot T_{2} = m_{2} \times a_{2}$

$\[ 2 \cdot T_{2} <a href=$ = m_{2} \times g - m_{2} \times a_{2} \]" src="https://idschool.net/wp-content/ql-cache/quicklatex.com-1e86b47f4eeb36e92d455be3e9cbfa99_l3.svg" style="height:14px; width:165px" title="Rendered by QuickLaTeX.com" />

$\[ T_{2} <a href=$ = \frac{m_{2} \times g - m_{2} \times a_{2}}{2} \]" src="https://idschool.net/wp-content/ql-cache/quicklatex.com-70f606759686bbde5302c2bf9fb219ea_l3.svg" style="height:27px; width:148px" title="Rendered by QuickLaTeX.com" />

Diperoleh dua persamaan berikut.

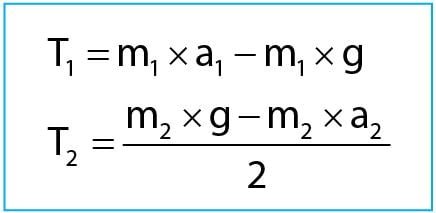
Persamaan Tegangan Tali pada Katrol Bebas 1

Demikianlah cara mendapatkan persamaan-persamaan gaya tegangan tali yang terdapat pada sistem katrol.

Rumus Percepatan Gerak Benda pada Katrol Bergerak

Kita akan membutuhkan cara mendapatkan rumus persamaan yang berlaku pada sistem katrol untuk menentukan percepatan gerak benda pada katrol bergerak. Kita hanya ambil salah satu kondisi. Untuk kondisi yang lain memiliki cara yang sama, hanya tandanya yang berbeda.

Perhatikan gambar sistem katrol yang diberikan di bawah.

Rumus Percepatan pada Katrol Bergerak

Gambar sebelah kiri menunjukkan kondisi awal sistem. Sedangkan gambar sebelah kanan menunjukkan kondisi sistem setelah beberapa waktu. Terlihat bahwa benda ke dua turun ke bawah dan benda pertama naik ke atas.

Apakah percepatan naik benda pertama sama dengan percepatan turunnya benda ke dua? Di sini akan kita selidiki kasus tersebut.

Lintasan yang dilalui benda 1 dan benda 2 memenuhi gerak lurus berubah beraturan, sehingga memenuhi persamaan.

$s = v_{0} \cdot t + \frac{1}{2} \cdot a \cdot t^{2}$