Grafik Persamaan Fungsi Trigonometri
Fungsi f dengan wilayah R dikatakan periodik apabila ada bilangan  , sedemikian sehingga
, sedemikian sehingga  , dengan
, dengan 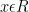 . Bilangan positif p terkecil yang memenuhi
. Bilangan positif p terkecil yang memenuhi  disebut periode dasar fungsi f.
disebut periode dasar fungsi f.
Jika fungsi f periodik dengan periode dasar p, maka periode-periode dari fungsi f adalah , dengan n adalah bilangan asli. Jika f dan g adalah fungsi yang periodik dengan periode p, maka
dan fg juga periodik dengan periode p.
1. Periode fungsi sinus dan kosinus
Untuk penambahan panjang busur dengan kelipatan
(satu putran penuh) akan diperoleh titik p(a) yang sama, sehingga secara umum berlaku :
dengan k∈B atau
dengan k∈B
dengan k∈B atau
dengan k∈B
Dengan demikian, fungsi sinus vatau
dan fungsi kosinus
atau
adalah fungsi periodik dengan periode dasar
atau
.
Baca Juga :
Pengertian Trigonometri dan Rumus Trigonometri Lengkap dengan Soal
Perbandingan Trigonometri dan Tabel Trigonometri Lengkap
2. Periode fungsi tangen
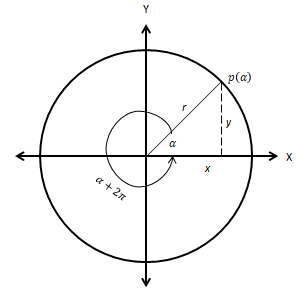
Untuk penambahan panjang busur dengan kelipatan
(setengah putran penuh) akan diperoleh titik
yang nilai tangennya sama untuk kedua sudut tersebut, sehingga secara umum
dengan
atau
dengan
.
Dengan demikian tangen atau
adalah fungsi periodik dengan periode
atau
.
Grafik Fungsi Trigonometri
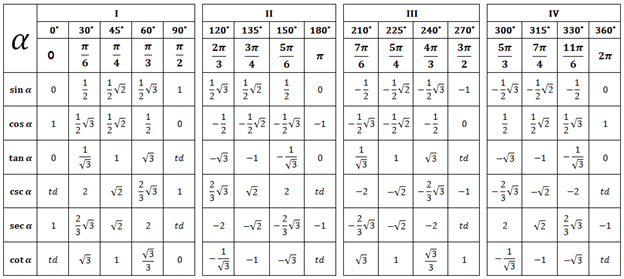
Dengan td adalah tidak didefinisikan. Untuk memudahkan, maka lihatlah segitiga berikut :
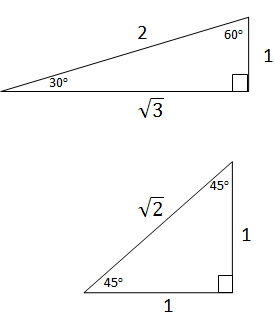
Dari konsep segitiga tersebut diperoleh nilai setiap sudut dan
. Untuk sudut
dan
diperoleh dengan cara berikut :
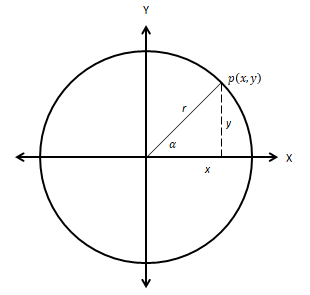
Didapat :
Jika titik bergerak mendekati sumbu X positif, akhirnya berimpit dengan sumbu X, maka x=r, y=0,
dan
, sehingga
Jika titik P(x,y)bergerak mendekati sumbu Y positif, akhirnya berimpit dengan sumbu Y, maka
, dan
, sehingga
- tan
= tidak didefinisikan
Nilai Maksimum dan Minimum Fungsi Trigonometri
Untuk setiap titik P(x,y) pada fungsi trigonometri memiliki hubungan :
dan
dan
dan
Berdasarkan uraian tersebut dapat dikemukakan bahwa :
Nilai maksimum dan minimum fungsi sinus
- Fungsi sinus
memiliki nilai maksimum
yang dicapai untuk
dengan
dan nilai minimum
yang dicapai untuk
dengan
.
- Fungsi sinus
memiliki nilai maksimum
yang dicapai untuk
dengan
dan nilai minimum
yang dicapai untuk
dengan
.
Nilai maksimum dan minimum fungsi kosinus
- Fungsi kosinus
memiliki nilai maksimum
yang dicapai untuk
dengan
dan nilai minimum
yang dicapai untuk
dengan
.
- Fungsi kosinus
memiliki nilai maksimum
yang dicapai untuk
dengan
dan nilai minimum
yang dicapai untuk
dengan
.
Secara umum dapat dikemukakan bahwa :
- Jika fungsi sinus
, maka nilai maksimumnya
dan nilai minimumnya
- Jika fungsi kosinus
, maka nilai maksimumnya
dan nilai minimumnya
-
Jika
adalah fungsi periodik dengan nilai maksimum
dan minimum
, maka amplitudonya adalah :
Jenis Grafik Fungsi Trigonometri
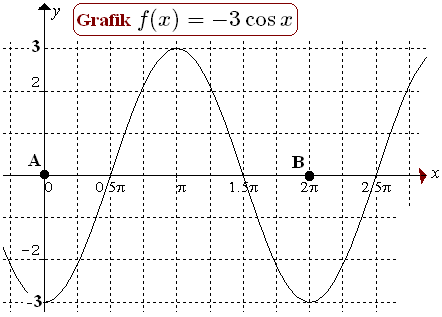
1. Grafik fungsi baku  ;
;  ; dan
; dan 
Sinus
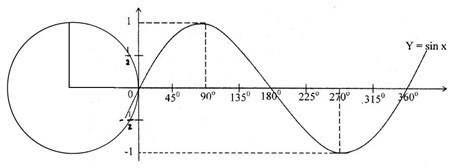
Cosinus
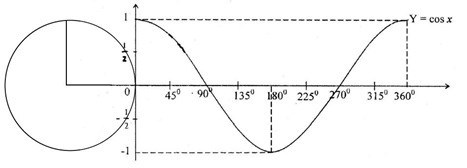
Tangen
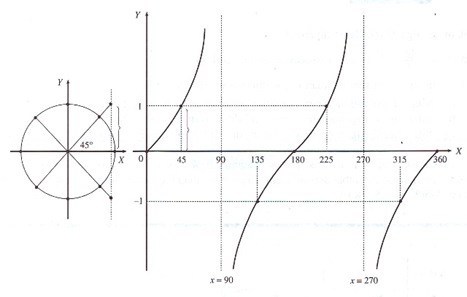
2. Grafik fungsi 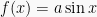 ;
;  ; dan
; dan 
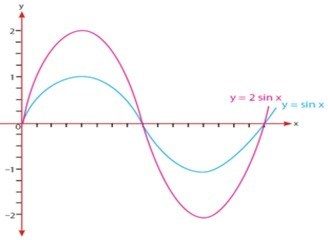
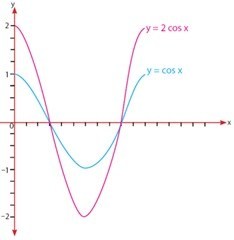
Didapat dari grafik trigonometri baku dengan cara mengalikan koordinat setiap titik pada grafik baku dengan bilangan a, sedangkan absisnya tetap. Periode grafik tetap untuk kosinus dan sinus. Sedangankan periode tangen
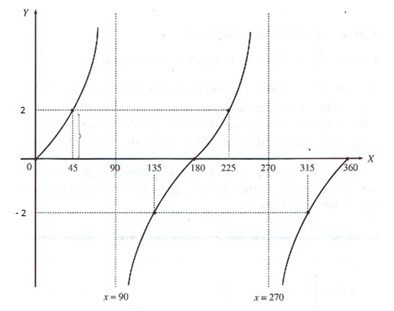
.
Sinus
Misalkan , maka grafiknya :
Kosinus
Misalkan , maka grafiknya
Tangen
Misalkan, maka grafiknya
3. Grafik fungsi 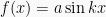 ;
; 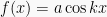 ; dan
; dan 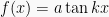
Didapat dari grafik trigonometri baku dengan cara mengalikan ordinat setiap titik pada grafik baku dengan bilangan a, sedangkan periode grafik sinus dan kosinus menjadi :
Dan tangen
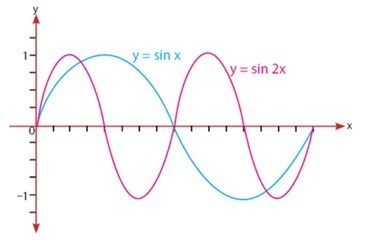
- Sinus
Misalkan dan
, maka grafiknya
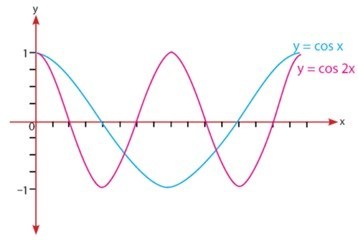
- Kosinus
Misalkan dan
, maka grafiknya
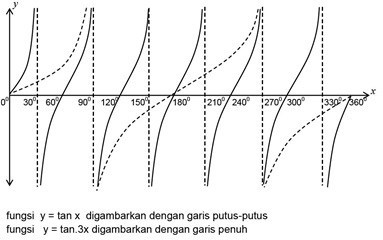
- Tangen
Misalkan a=1 dan k=3
, maka grafiknya
- Jika fungsi kosinus
, maka nilai maksimumnya
dan nilai minimumnya
Jika adalah fungsi periodik dengan nilai maksimum
dan minimum
, maka amplitudonya adalah :
Dengan demikian, fungsi sinus vatau
dan fungsi kosinus
atau
adalah fungsi periodik dengan periode dasar
atau
.
Artikel Terkait
- asd
- asd
- Sinonim akulturasi adalah kontak kabudayaan #sinonim #bahasa #akulturaasi #bahasaindonesia #antonim
- Pada Suatu Pertemuan, Hadir 10 Orang yang Saling Berjabat Tangan. Banyaknya Jabat Tangan yang Terjadi Adalah... Jawaban dan Pembahasan
- Suku Kelima Suatu Barisan Aritmatika Adalah 22, Sedangkan Kesembilan Adalah 42. Suku Kelima Belas Sama Dengan... Jawaban dan Pembahasan
- Mata Uang yang Sering Digunakan Sebagai Alat Pembayaran dan Kesatuan Hitung Dalam Transaksi Ekonomi dan Keuangan Internasional Disebut...
- Kingdom yang Tidak Memiliki Dinding Sel... Jawaban dan Pembahasan
- Organel Sel yang Berperan Untuk Mendetoksifikasi Racun Adalah... Jawaban dan Pembahasan
- Diketahui Harga 4 kg Jeruk, 1 kg Semangka, dan 2 kg Apel Adalah Rp 54.000,00. Harga 1 kg Jeruk, 2 kg Semangka, dan 2 kg Apel Adalah Rp 43.000,00. Sedangkan Harga 3 kg Jeruk, 1 kg Semangka, dan 1 kg Apel Adalah Rp 37.500,00. Berapakah Harga 1 kg Semangka?
- Nilai Rataan Hitung dari Data 4 10 7 x 10 6 11 Adalah 8 Nilai x Adalah ...